Author: Guancheng Li of Tencent Xuanwu Lab

在当今数字世界中，RSA‑2048 与 ECC 等经典公钥密码是最广泛应用的加密标准，支撑着网络安全、金融交易和隐私保护的底层信任。然而，这一基石正面临量子计算的潜在威胁。理论上，量子计算机能够以远快于经典计算机的速度分解大整数和离散对数求解，从而在短时间内破解 RSA 和 ECC 加密。这一前景既令人兴奋，也令人担忧。

问题在于：量子计算机的发展究竟到了什么阶段？有人乐观地认为经典公钥密码的“倒计时”已经开始；也有人怀疑，受限于制造难度，真正可用的量子计算机还遥遥无期。市面上相关论调不一，往往乐观或悲观，但核心疑问始终萦绕：量子计算机距离破解经典公钥密码还有多远？

首先，为帮助读者理解量子计算的原理，我们会介绍必要的量子力学概念，如量子态与纠缠，并解释为什么量子计算机能够在特定问题上实现加速；其次，为了让大家对量子计算机的形态与实现路径有直观认识，我们将解析其基本构造，并重点拆解目前发展最快、工程上最具可行性的超导量子计算机的内部结构；最后，我们会以超导量子计算机为例，深入分析其在迈向破解经典公钥密（RSA‑2048）的过程中仍面临的瓶颈，以及这些问题背后潜在的解决希望。

我们的结论是：科学层面已不存在“死胡同”，真正的挑战集中在工程实现。冷却、控制、布线、能耗与量子纠错的实时实现仍是巨大难关，但随着规模扩展与模块化设计的推进，这些问题有望逐步缓解。综合当前趋势，我们认同业界普遍预测：百万量子比特级量子计算机极可能在 203X 年出现，届时经典公钥密码的防线将大概率被攻破。这也意味着，后量子迁移工作必须尽早启动。一方面，“先存后解”（Store Now, Decrypt Later）攻击模式已经现实存在，敏感数据即使今天被窃取，也可能在未来被量子计算解密；另一方面，密码体系迁移本身是一个涉及算法替换、系统改造、标准合规和生态适配的庞大工程，通常需要多年才能完成。若等到量子计算机真正快要问世时才行动，往往已为时过晚。

本文也发布于“科普中国”和“腾讯后量子密码主题站”。顺带打个广告，该网站还有后量子迁移指南、行业动态追踪、后量子密码学标准、算法性能评测等优质内容，欢迎关注！👏

Part 1: 量子计算机为什么能加速计算？

量子计算机的核心优势在于其利用了量子叠加性和量子纠缠性。为了理解其对计算的加速，首先需要了解量子物理的基础特性——叠加态、坍缩和量子纠缠。

注：为了让不熟悉数学或物理的读者也能理解，本部分会尽量不使用数学公式，这样做可能会带来一些细节上的不准确，但不会影响整体理解。对于具备一定的数学基础的读者，可以对照附录1一起阅读，附录以数学形式对叠加态，坍缩以及纠缠等现象作了更直观的说明。

叠加态与坍缩

在经典物理中，系统的状态（例如位置、速度）在任意时刻都是确定的；而在量子力学中，粒子的情况则不同。一个粒子的某一物理量（如位置、动量、自旋、能级等）在未被测量之前，并不处在某一个具体的值，而是一个同时包含所有可能的结果的叠加态。只有在测量时，这个叠加态才会按照某种概率瞬间变成某个固定的值。

举一个简单的例子：设想有两个小盒子，粒子只能出现在其中一个盒子里。按照经典的直觉，它要么在左边的盒子里，要么在右边的盒子里，永远不会同时在两个地方。但在量子实验中发现，在没有测量之前，粒子并不是已经待在左边或者右边，而是处在一种同时“包含左和右可能性”的状态。只有当我们真正去测量时，粒子才会呈现为在其中一个盒子里。这个过程叫做坍缩。坍缩时，每一个可能的状态都会对应一个概率（概率需满足所有可能性的总和为 1，具体的概率分布是叠加态的性质之一）。例如，一个粒子可能处在如下的叠加态：

出现在左边的概率为 70%
出现在右边的概率为 30%

这听起来似乎难以置信，但叠加态的存在早已通过实验得到验证，一个经典的例子就是电子的双缝干涉实验，感兴趣的读者可以进一步查阅相关实验。

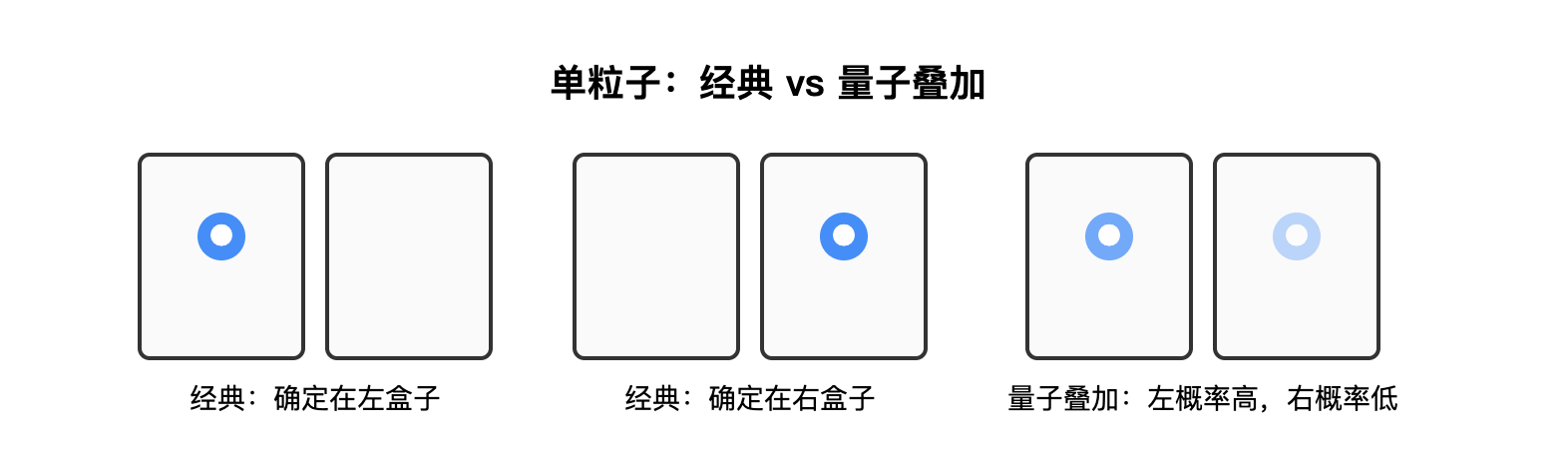
图：经典物理状态与量子叠加态的对比，量子叠加态的颜色代表其在测量时出现的概率。

基于这一原理，量子计算机从物理系统中选择两个可以明确区分的结果来作为信息的基本单位。例如，可以规定“粒子在左盒子里”为 0，“粒子在右盒子里”为 1。这样，一个量子比特在未被测量时，并不是单纯的 0 或 1，而是同时包含两种可能性。当测量发生时，它才会确定为其中之一。这意味着，量子比特能够在未测量时以叠加的形式同时携带 0 和 1 的信息，这是它区别于经典比特的根本特征。

量子纠缠

在理解了单个物理量可以同时处于多种可能性的叠加之后，我们就可以进一步讨论量子纠缠。量子纠缠是一种超越经典直觉的量子关联现象。当两个或多个粒子的某些属性（例如它们所在的位置）发生纠缠时，这些属性不再是彼此独立的，而是形成一个不可分割的整体。

举个例子：设想有两只相同的小盒子，一个在左边，一个在右边。我们现在放入两个粒子，分别编号为 1 号和 2 号。按照经典的直觉，可能的情况有四种，每种都有一定的发生概率：

两个粒子都在左边（记作 LL）
两个都在右边（记作 RR）
1 号在左、2 号在右（记作 LR）
1 号在右、2 号在左（记作 RL）

经典物理会认为，粒子一定处于其中一种确定的组合，只是我们暂时不知道是哪一种。

但在量子物理中，如果两个粒子的位置发生了“两个粒子所在的盒子必须不同”的纠缠，那么情况就完全不同。在测量之前，它们并不是已经固定在某一种组合，而是处在一种整体性的叠加状态。在这种状态下，只允许两种可能性同时存在：

1 号在左、2 号在右（LR）
1 号在右、2 号在左（RL）

当我们真正去测量时，系统会瞬间“坍缩”为其中之一：要么是 LR，要么是 RL。每一种情况都有一个对应的概率（概率不必相等，概率分布是纠缠态的固有性质之一）。与此同时，LL 与 RR 的结果概率为零。可以看出，纠缠后的量子态其实是一个更为全局的叠加态。量子纠缠也是通过物理实验得到验证的，感兴趣的读者可以进一步查阅相关资料（关键词：EPR佯谬，贝尔不等式）。

图：经典粒子组合与粒子纠缠之间的对比

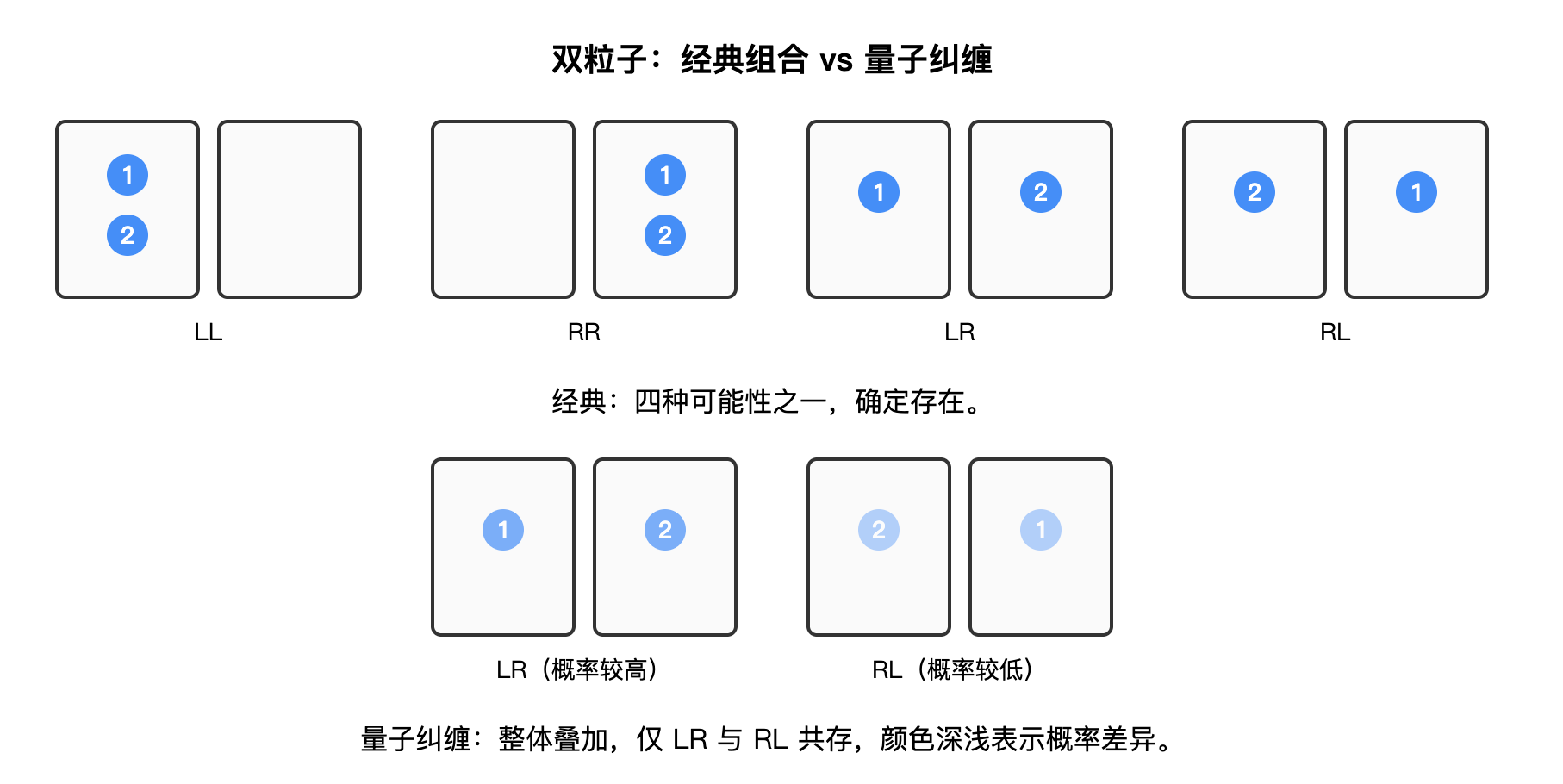
将这一原理应用到量子比特上（比如我们认为 L 是 0，R 是 1），我们就可以制备出一种“两个比特的取值必须不同”的纠缠状态。在这种状态下，两个比特在测量之前，并不是确定地处在“01”或者“10”，而是这两种可能性的叠加。等到测量发生时，系统会瞬间坍缩为某一个确定的结果：要么得到“01”，要么得到“10”。与此同时，“00”与“11”这两种组合完全不会出现，它们的概率为零。

利用叠加性和纠缠性加速计算

叠加性赋予量子比特在未测量时同时处于多种状态的能力，纠缠性使得量子比特之间能够形成非经典的强关联，这种关联在许多量子算法和量子误差校正中是不可或缺的核心资源。

在这里，我们给出一个直观的例子来帮助理解。假设我们有一个由 $n$ 个量子比特组成的系统，用它来表示一个输入变量 $x$。由于叠加原理，$x$ 的状态可以同时覆盖从 $0$ 到 $2^n-1$ 的所有可能取值，而不仅仅是某一个具体数。当我们将这样的量子态输入到函数 $f(x)$ 中时，输出也会成为所有可能输入对应结果的叠加态。

如果我们想寻找满足 $f(x)=c$ 的 $x$ 的值，就可以通过精心设计的量子算法（涉及对量子纠缠和量子干涉等机制的利用），增强正确结果对应的概率振幅，同时削弱错误结果的概率振幅。这样，在最终测量时，就能够以更高概率得到正确答案。需要强调的是，这种“放大正确解概率”的过程，正是量子算法的核心思想之一。

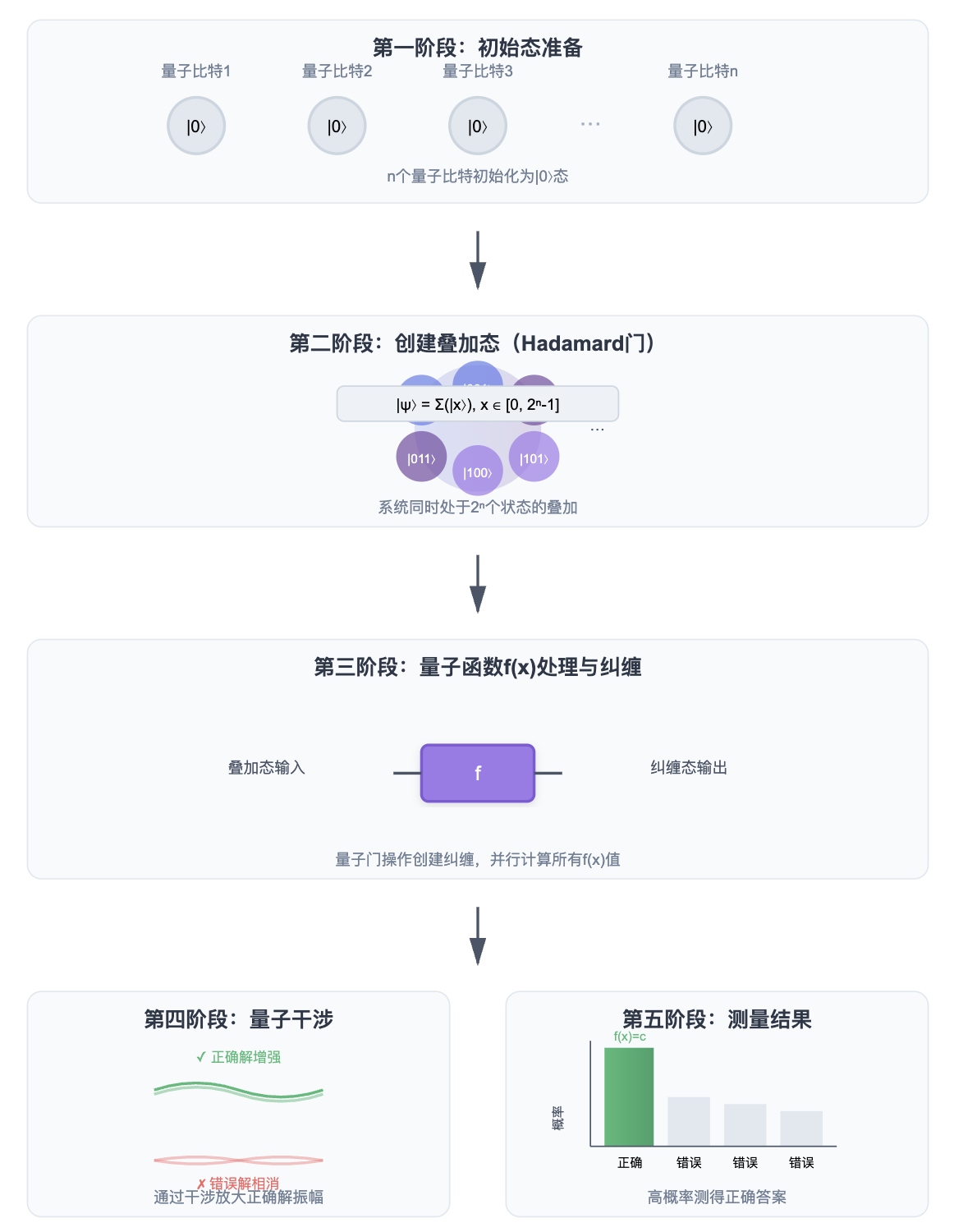
图：量子计算的核心思想，通过叠加实现并行计算，通过纠缠和干涉放大正确解的概率

注：在提到量子干涉时，我们实际上默认了量子态可以用波的形式来表示。为了照顾不熟悉数学或物理的读者，我没有展开说明这一点。如果读者对“为什么微观物理量能够以波的形式来描述”感兴趣，可以参考附录1。

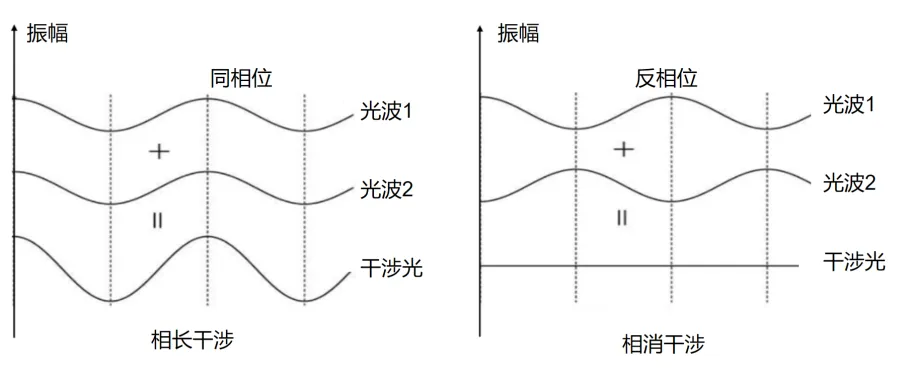
图：干涉是波的叠加效应。当两个正弦波的波峰重合时，会产生相长干涉，叠加后的振幅增大；反之，则会发生相消干涉，振幅减小。我们所熟悉的降噪耳机就是利用相消干涉来抵消噪音，量子计算也可以通过相长干涉放大正确答案的概率振幅，通过相消干涉缩小错误答案的振幅。

当然，现实中的量子算法远比这个直观描述复杂得多，这里我们仅作简化说明，暂不涉及具体算法细节。若读者希望进一步了解量子算法为何会对经典密码体系构成潜在威胁，可以参见附录2。

量子计算对不同问题的加速效果

量子计算机所带来的加速的主要来源是

叠加态，即 $n$ 个量子比特可以同时表示 $2^n$ 个状态，相当于一次性并行处理所有可能性。
纠缠，通过量子比特间的强关联，使不同状态间发生干涉，从而有效提取有用信息、放大正确答案。

而这种加速在不同类型的问题上体现得不同，在有合适量子算法的情况下：

有结构的问题（如质因数分解）：量子算法可以利用其结构（如周期结构），通过某种算法（如量子傅里叶变换）快速提取答案，从而实现指数级加速。
无结构的问题（如寻找满足 $f(x)=c$ 的 $x$）：由于没有规律可利用，只能依靠连续 $\sqrt{N}$ 次干涉放大正确答案的概率幅，因此计算次数只能从经典的 $N$ 次降到 $\sqrt{N}$ 次，对应平方根级加速。

Part 2: 量子计算机是怎样构建出来的？

量子比特在物理上的实现方式

量子比特本质上是由物理世界的状态构建而来的。根据所使用的物理状态的来源不同，量子计算机的构建方法可以划分为两大类：

第一类量子计算机基于微观粒子，如离子、光子或原子，通过操纵和测量它们的量子态来计算。同类型的微观粒子在物理性质上完全一致，这对多粒子量子干涉和纠缠的实现中具有重要作用。同时，这些粒子在良好隔离条件下能保持较高的量子态纯度、较低误差以及较长的相干时间（即量子态的保持时间)。然而，对这些粒子的精准操作在当前技术水平下难度仍然很大，且操作所需的时间通常较长。

第二类是基于人造结构的量子计算机，比如超导电路、量子点等，将人造结构的微观状态的宏观体现作为量子态。这类方法的优势在于易于制造和操作，且可以借助现代半导体技术进行扩展。但人造材料的缺陷是一大挑战。与天然粒子不同，每个人造结构都有细微差异，这种差异可能引入额外的噪声或错误，影响量子态的稳定性。不过，相比微观粒子，人造结构的量子比特更容易被测量和操控，在工程上更具可行性。

图：量子计算机的两大类构建方法

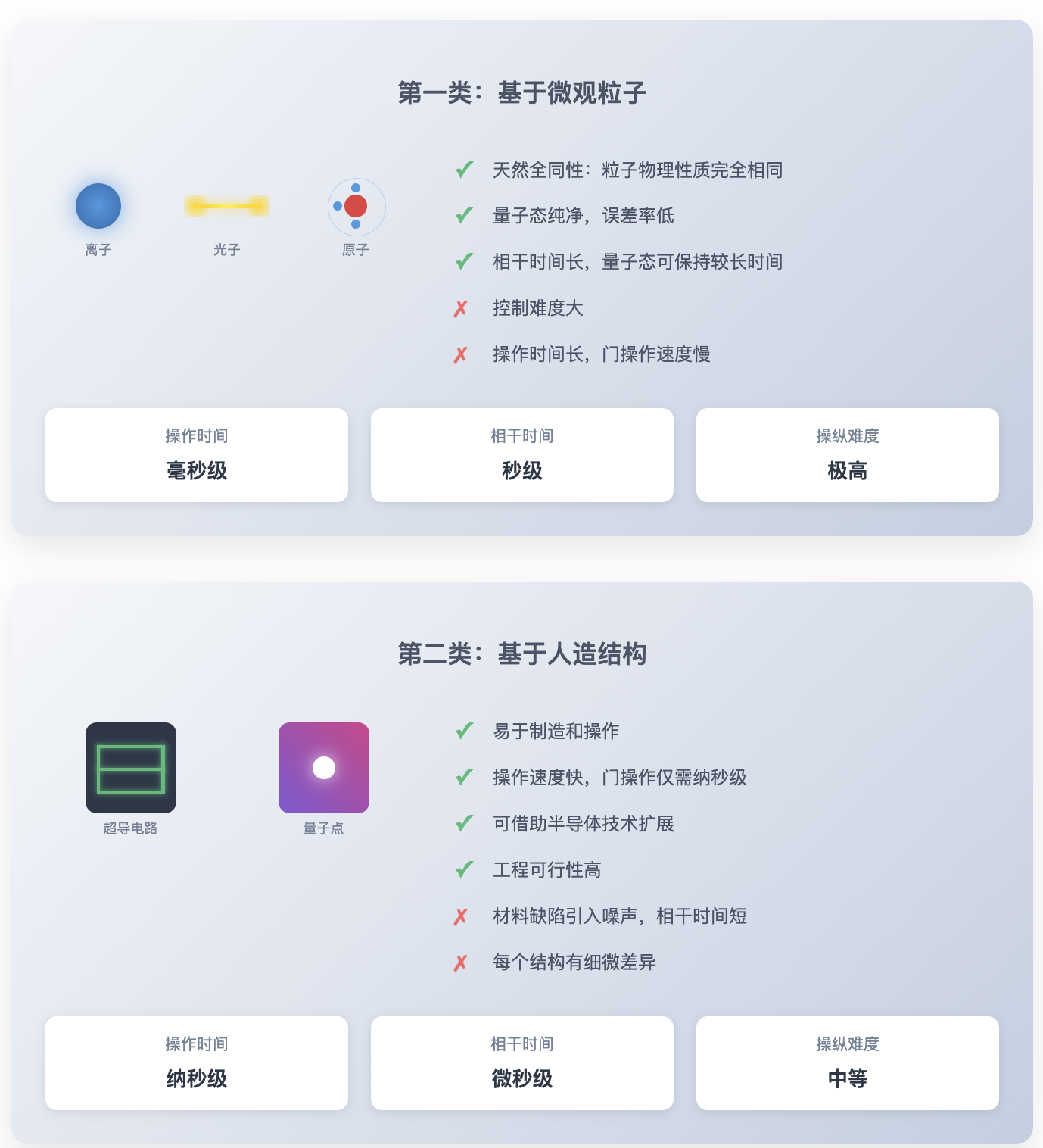
目前，超导量子计算被认为是最成熟和最有前景的方向之一，因为它在操作速度和集成度方面表现优异，且技术发展相对迅速，因此我们接下来将重点以超导量子计算机为例进行展开介绍。

超导量子比特的构建原理

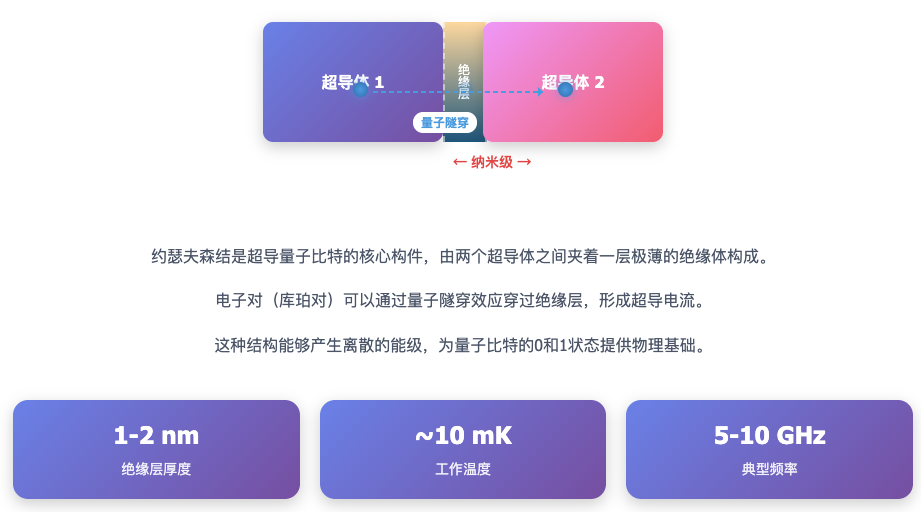
具体到超导量子计算机，量子比特的状态来源于其核心构件“约瑟夫森结”的“能级”。约瑟夫森结是由两个超导体之间夹着一层纳米级的绝缘体构成。而能级是物理系统可以拥有的能量值，其特点是离散的、固定的，系统的能量只能处于这些特定值之一，例如 E₀ 、 E₁ 等，而不能连续变化，这种现象是量子力学的基本特性之一。最低的能级 E₀ 通常被称为“基态”，更高的能级（如 E₁）被称为“激发态”。量子比特的两个基本状态——0 和 1，分别对应于系统的基态 E₀和第一个激发态 E₁。

图：约瑟夫森结构造原理

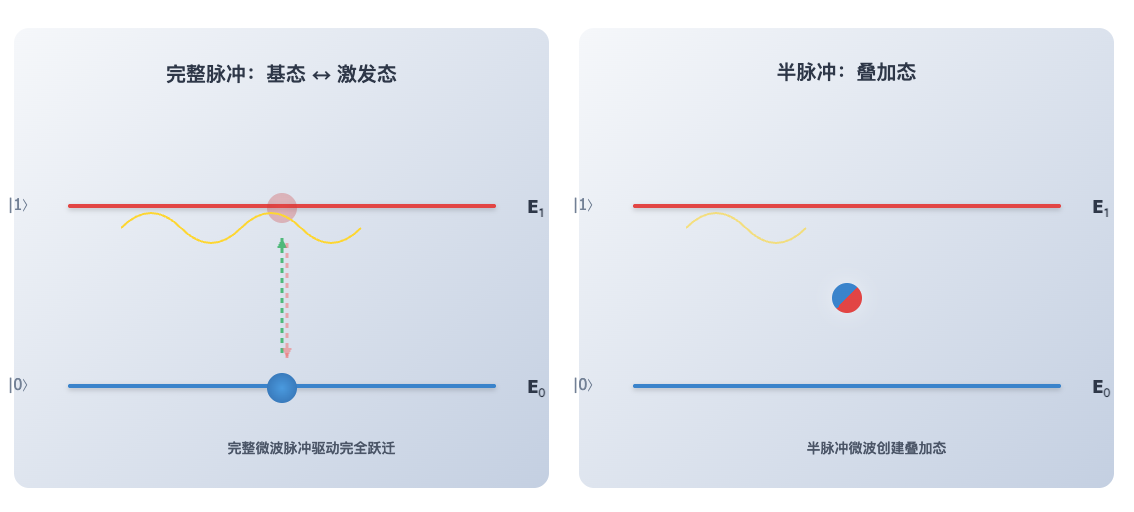
通过向约瑟夫森结施加特定频率的微波信号（微波是一种电磁波，可以传输能量。比如微波炉通过特定频率的微波驱动食物中的水分子等极性分子快速旋转和振动，使其相互作用产生热量，从而加热食物），可以向系统注入能量，使量子比特从较低的能级 E₀ 跳跃到较高的能级 E₁，或者通过释放能量从 E₁ 返回到 E₀。这种对能级跃迁的精确控制，是量子计算中实现基本逻辑操作的关键。更进一步，如果只施加一个“半脉冲”的微波信号——即没有完全驱动量子比特从 E₀ 跳到 E₁，而是恰好停在中间态，那么量子比特就会处于 E₀ 与 E₁ 的叠加态。总结来说，我们可以通过调节微波的频率、强度和持续时间，精确控制量子比特的状态。

图：超导量子比特的能级跃迁与控制。完整脉冲提供恰好的能量使量子比特从基态E₀完全跃迁到激发态E₁，实现|0⟩ → |1⟩的转换。半脉冲只提供部分能量，使量子比特处于E₀和E₁的叠加态，即同时处于|0⟩和|1⟩的量子叠加。通过调节微波的频率、强度和持续时间，可以精确控制量子比特的状态

由于超导量子比特的能级之间的能量差极其微小，因此量子态对外界环境的扰动极为敏感。哪怕是极轻微的热噪声、电磁波或辐射干扰，都可能导致量子态的退相干（即量子态被破坏），从而使量子比特无法正常工作。为了降低这些干扰，超导量子计算机必须运行在接近绝对零度的极低温环境下（约 10毫开尔文（mK），比绝对零度-273.15 °C只高出 0.01 度，已经是人类能实现的最低持续温度），并在连接线路中使用特殊材料和精心设计的屏蔽、滤波与衰减措施，以尽可能保持能级稳定和操控精度。

从单比特到超导量子计算的“体系结构”

要构建一台可实际运行的超导量子计算机，不仅需要量子比特本身，还必须有完整的支撑系统：制冷和屏蔽系统用于保护量子态，控制系统用于操控量子比特，纠错系统用于实时纠正量子系统中的错误。在这些系统中，纠错系统尤为关键。这是因为量子计算的可靠性面临两个根本性挑战：

相干时间不足：即量子比特能够保持叠加态和纠缠等量子特性不被环境破坏的时长，因此要用量子比特执行计算，量子比特的相干时间必须长于计算所需的时间。制冷、屏蔽等措施虽然能延长相干时间，但对于复杂运算仍难以满足需求。
门保真度不足：量子门不是像经典比特那种固定的门电路，而是通过外部控制信号实时操控来实现，量子门操作的实际效果与理想效果的接近程度即为门保真度。然而，即使单个门操作的保真度很高（如99.9%），在执行成千上万次操作后，误差仍会不断累积，最终破坏计算结果。

接下来，我们会详细介绍超导量子计算机的每一个核心组成部分：

量子芯片

采用传统半导体工艺在硅片上制作出约瑟夫森结，形成量子比特，并通过封装引出用于控制和测量的接口。

图：一个拥有 20 个超导量子比特的量子芯片（又称量子处理器）示意图，可以看到每个量子比特都需要引出多根线缆（比如控制线、读出线），同时量子比特与比特之间还需要有耦合器（类似于开关）互联

制冷系统

利用稀释制冷机（一种利用氦‑3/氦‑4 混合物实现超低温的降温设备，目前是人类能够持续运行并达到最低温度的制冷装置，可将温度降至约 10 mK 甚至更低）将量子芯片及其连接线降温至接近绝对零度，同时配置衰减器、滤波器来“净化”控制信号，配置屏蔽装置屏蔽外部噪声，以尽量消除外部噪声干扰。

图：IBM Q量子计算机的制冷系统结构。整个结构会被放置到稀释制冷机中，可以看到，其中包含用于控制和读取量子比特的微波导线；输入信号经过多级衰减器以降低噪声，输出信号则通过低噪声放大器放大；同时配备多层屏蔽装置以隔绝外部辐射，并使用经过精心选择材质的同轴电缆以保证在低温下的可靠传输并最小化热负载。从系统顶部到底部，温度逐级降低：最上层为室温区，最底层则可达到约 10 mK 的极低温环境，为量子比特的稳定运行提供条件。

量子比特控制系统

将经典计算机发出量子操作的指令转化为高精度微波脉冲，用于驱动、操控与读出量子比特，通常包含微波发生器、混频器、放大器和隔离器等器件。

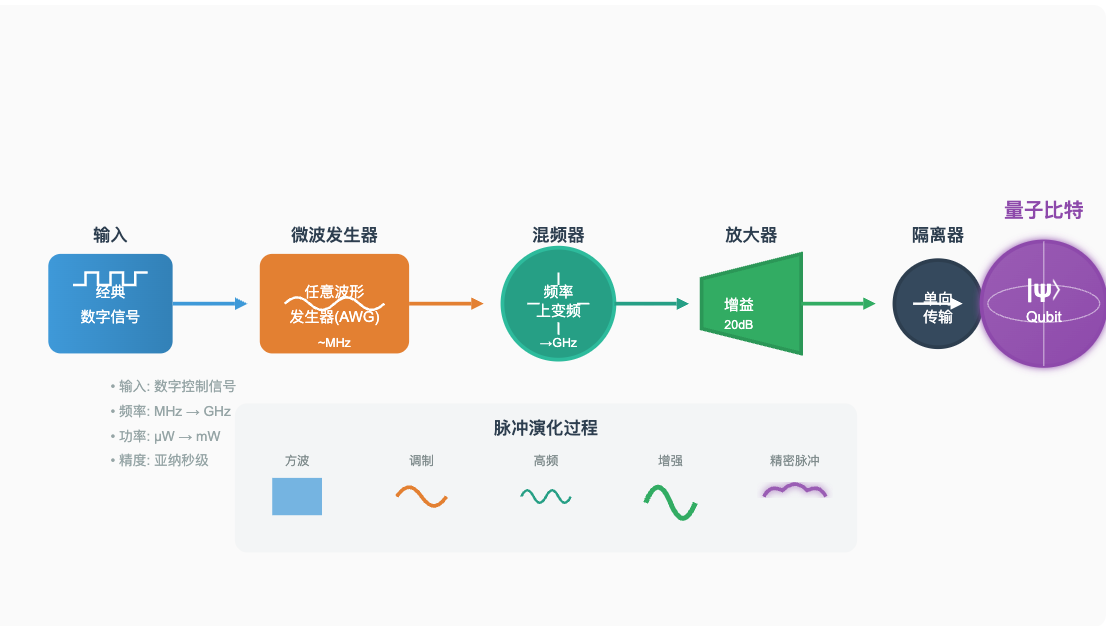
图：量子比特控制系统接收来自经典计算机的数字控制信号，通过一系列精密的微波器件，将其转换为能够精确操控量子比特的微波脉冲。系统的核心在于保持极高的信号纯度和时序精度，确保量子态的精确操控。将经典数字信号转化为高精度微波脉冲，用于驱动、操控与读出量子比特。

量子纠错系统

通过冗余编码和实时反馈，检测并修正量子计算过程中因退相干和噪声产生的错误，从而延长相干时间和提升门保真度。例如，目前最为常用的表面码纠错方案通过把一个逻辑量子比特编码到一个二维量子比特阵列中，通过不断测量邻近比特之间的关联来发现并修正错误，从而在硬件误差率低于阈值的情况下延长逻辑比特的寿命。

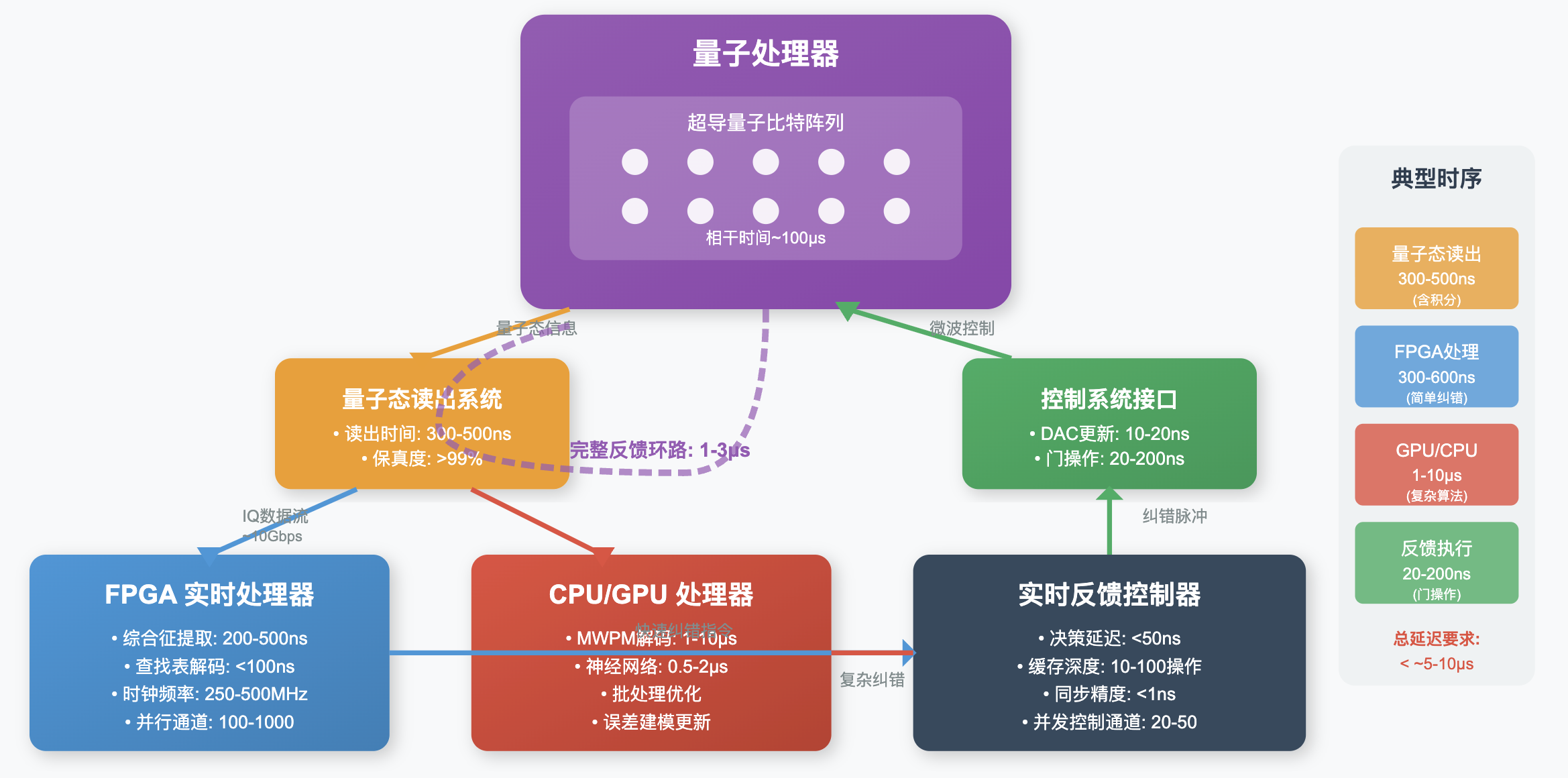
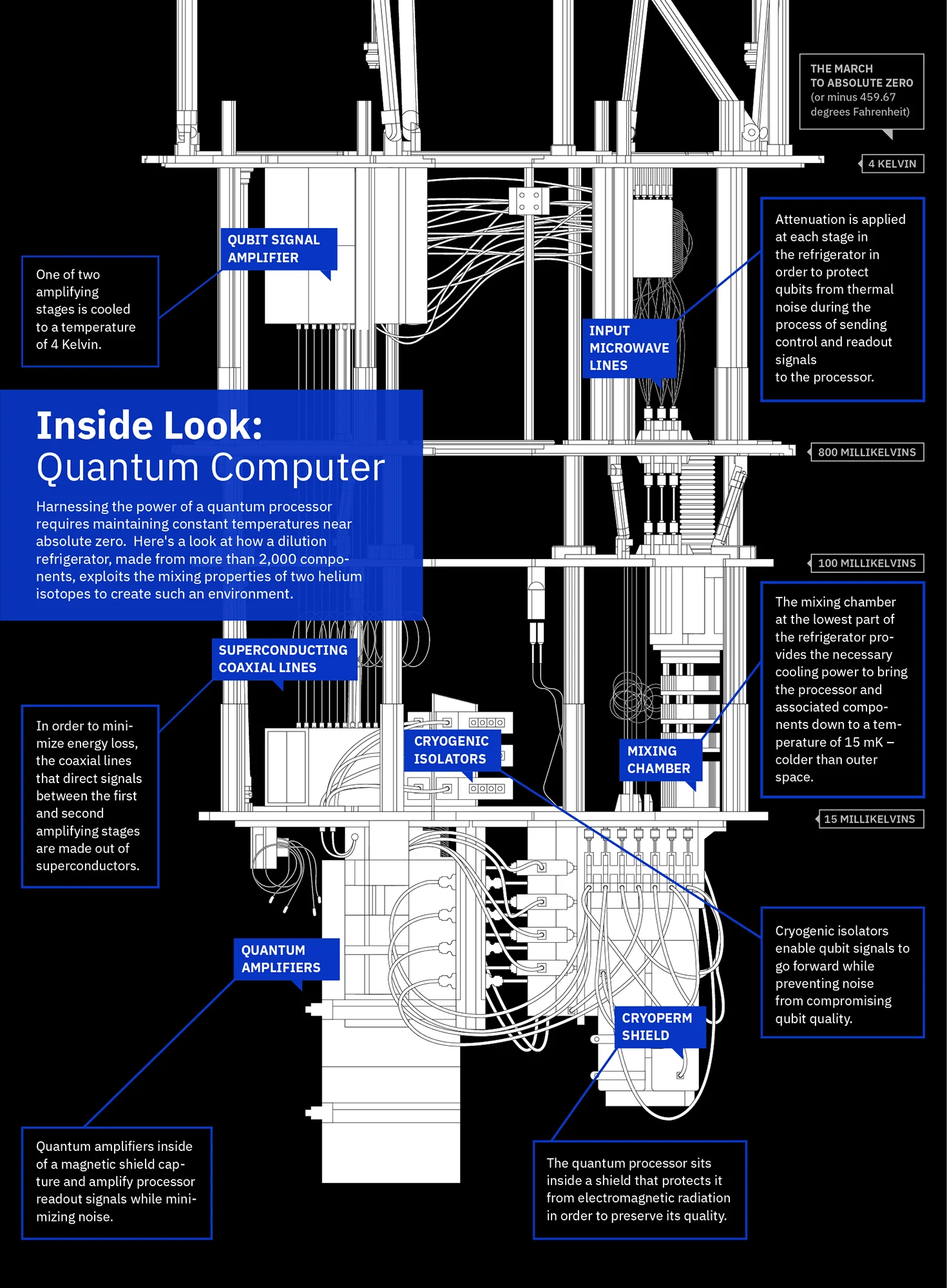
图：量子纠错系统是一个经典-量子混合系统，整个纠错环路必须实时完成纠错，纠错时间要远小于退相干时间。FPGA的低延迟处理和CPU/GPU的强大算力相结合，配合精确的时序同步，确保在量子信息丢失前完成错误修正。

整体架构

从下图中，我们可以大致了解量子计算机的整体架构。

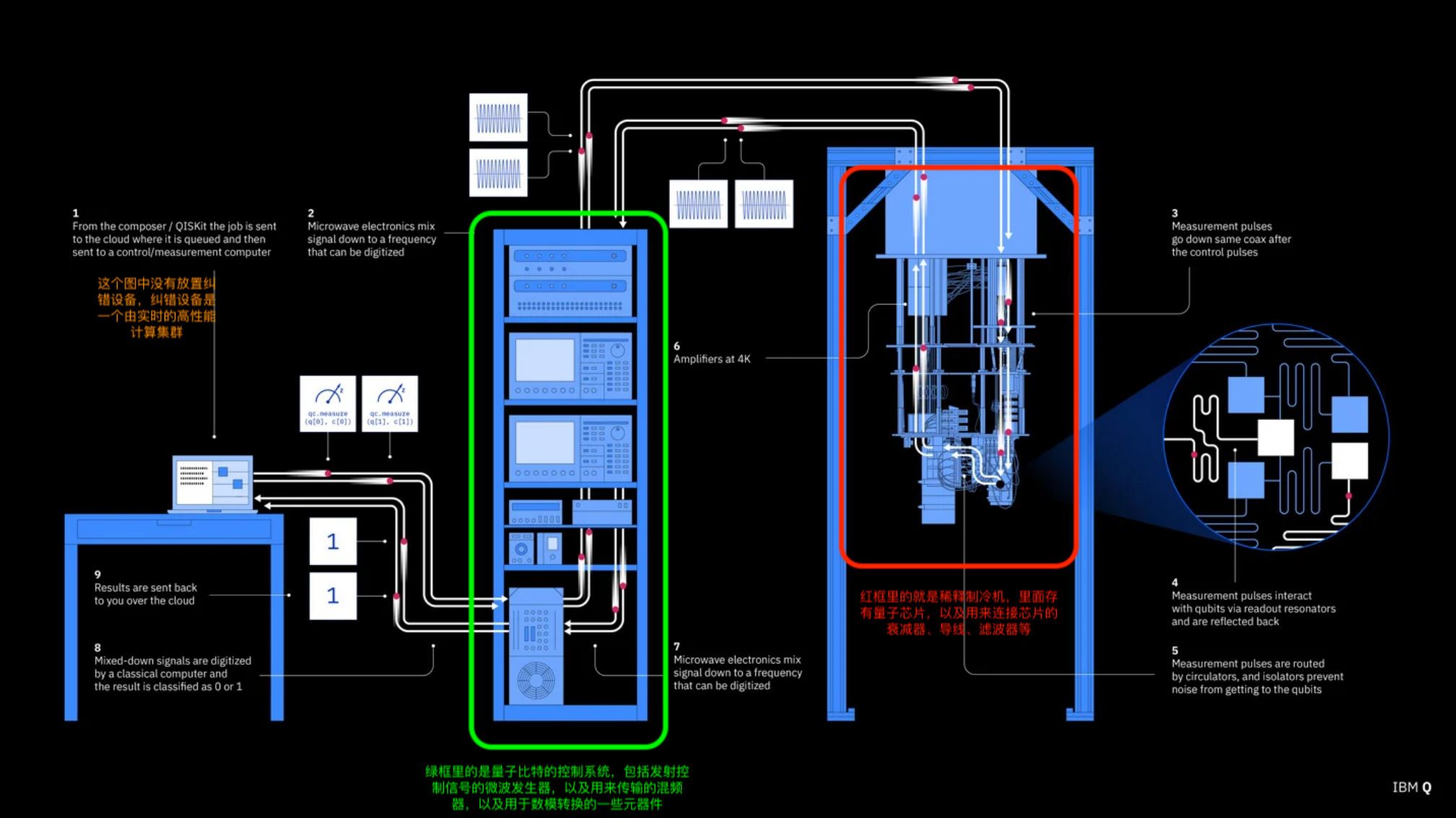
图: IBM Q量子计算机架构图，我们可以在图中找到我们所述的组成部分。

构建量子计算机需要科学与工程学结合

量子计算机的构建既是一门物理学，也是一门工程学。粒子型方案在物理层面更纯净，但工程实现困难；人造结构型方案（尤其是超导量子比特）在工程上更具可扩展性，但需克服噪声与退相干问题。一台完整的超导量子计算机，实质上是量子芯片 + 稀释制冷机 + 控制电子学 + 量子纠错系统的复杂组合。它既是物理实验装置，也是高度工程化的系统。正是因为具备这种“从物理到系统”的完整链路，超导量子计算机才成为当前最有希望率先跨越实用门槛的方案。

Part 3: 构建能破解 RSA 2048 的量子计算机，还有哪些挑战？

目前较为成熟的超导量子计算机的量子比特规模大多在数百个左右。正如在Part1提到，量子计算机在质因数分解上能够提供指数级加速，Shor 算法分解一个 N 位整数大约需要 2N个量子比特用于计算，再加上辅助寄存器和运算所需的额外开销，要破解 RSA-2048 整体规模约为数千个量子比特。

听起来似乎离成功不远了，对吧？其实并不是。要想让量子计算顺利完成破解，如前文所述，量子比特的相干时间必须长于完成所有必要运算所需的时间。然而，目前超导量子比特的相干时间通常只有几十到几百微秒，量子门操作时间在几十到几百纳秒，而Shor算法需要 10¹² 量级的量子门操作，因此计算时间将远远超过了量子比特的相干时间。即便能在相干时间内完成操作，也会受到门保真度的限制，即使单个门的保真度高达 99.9%，在 10¹² 次操作后微小误差也会不断累积，最终破坏计算结果。

因此，必须依赖量子纠错来突破这些物理瓶颈。以表面码为例，它通过将大量物理量子比特编码为一个逻辑量子比特，从而有效延长“可用的相干时间”，并抵消门操作中的累积误差。以目前的误差率和纠错方案来看，一个逻辑量子比特通常需要几千个物理量子比特。换句话说，要想获得几千个逻辑量子比特来运行 Shor 算法，实际需要的物理量子比特总数将达到百万级。

接下来，我们会详细介绍，要将超导量子比特的数量从数百个扩展到数百万个，量子计算机每一核心组成部分所需要跨越的技术障碍。

量子芯片

量子芯片，也就是放置量子比特（约瑟夫森结）的芯片，又称量子处理器。要构造更多量子比特的芯片，主要会遇到三个难题：布线问题、串扰问题和半导体良品率问题。

布线问题

由于每个量子比特都需要引出多根线缆（比如控制线、读出线），同时量子比特与比特之间还需要有耦合器（类似于开关）互联。在二维芯片上，当量子比特数量增加时，布线复杂度会非线性增加。特别是当需要实现高连接度时，中心区域的比特控制线必须绕过外围比特，导致芯片面积急剧增加。

图：随着量子比特数量增加，布线复杂度呈非线性增长

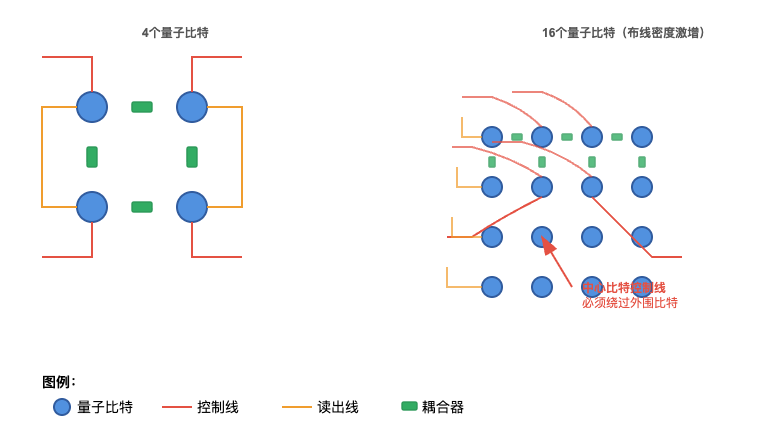
串扰问题

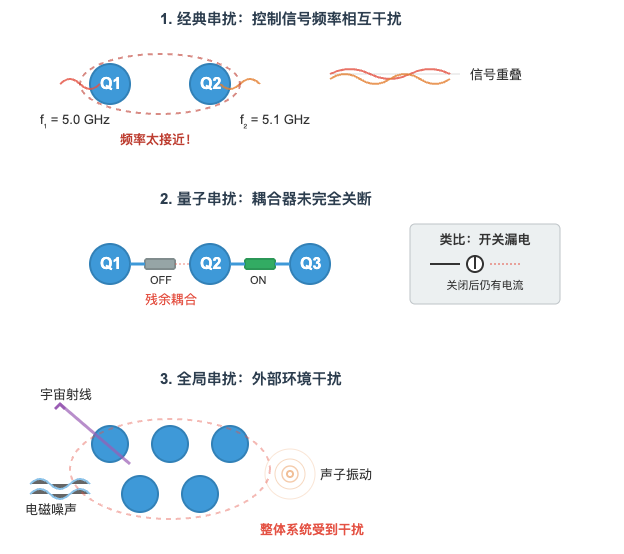
串扰指的是量子比特之间的互相干扰，会导致量子态退相干，并且随着比特数量的增加呈非线性增强。常见的串扰可以分为：

经典串扰：量子比特的控制信号的频率靠的太近，导致控制相互干扰。（频率指的是波每秒完成的周期数。在量子计算中，每个量子比特通过不同频率的微波信号进行控制，从而实现精确的操作和调控）
量子串扰：本应关闭的比特耦合没有完全关断；（类比到经典电路则是断开开关之后仍然还有电流通过）
全局串扰：来自外部环境的未知物理过程的串扰，比如宇宙射线，声子传播等

要避免串扰，一方面可能需要更大的隔离区或精心设计的屏蔽结构，另一方面也可以在器件层面优化耦合器（coupler）的性能，让比特间的耦合开关得以更彻底地关断。此外，改进测控系统，尤其是频率分配的优化，也有助于降低并行执行双比特门时的串扰。

图：串扰随量子比特数量增加呈非线性增强，严重影响量子态相干性。

器件良品率问题

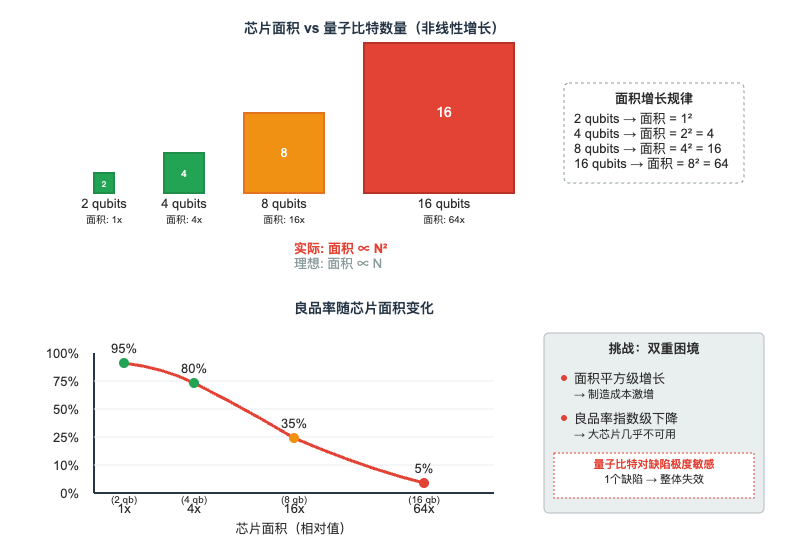
如果单从面积来看，量子芯片的面积应该和量子比特数量成线性关系。但由于要处理布线和串扰问题，实际芯片面积往往会随着量子比特的数量接近平方增长。也就是说，量子比特越多，芯片面积就会非线性地放大。

更麻烦的是，量子比特对缺陷极其敏感，哪怕 1% 的失败率都会让整个系统不可用。如果芯片内部或者表面存在缺陷，就可能与量子比特发生耦合，降低其相干时间。而在微纳加工领域存在一个基本规律：芯片面积越大，良品率越低，大面积芯片的制造难度会呈指数增加。对于超导量子芯片来说，虽然其制造过程可以借用半导体工业的成熟设备和工艺流程，但量子比特对制造缺陷的极端敏感性使得良品率问题成为一个巨大的挑战。

图：面积随着量子比特数量以N²增长，而良品率随面积指数下降。图中概率值仅作演示，非真实值。

希望的曙光：模块化设计与片间互联

布线、串扰和良品率的问题，都会随着量子比特数量的增加而非线性恶化。因此，如果直接在一块芯片上构造百万量子比特，几乎是不可能的。

于是出现了新的思路：先构造数千个物理量子比特的小芯片(chiplet)模块（这样就能组成一个可靠的逻辑量子比特），再通过片间互联技术把这些小芯片连接起来。这样一来，单片的工程挑战只是从数百扩展到数千，难度大幅降低，也更加可行。

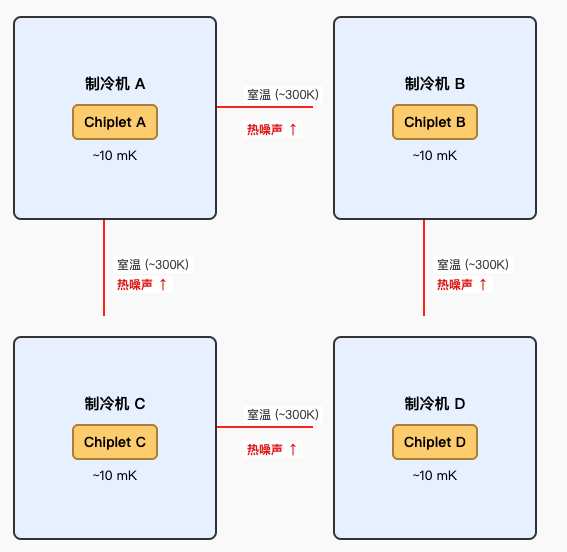
不过，这个思路也带来了新问题。量子比特非常脆弱，必须放在 10 毫开尔文左右的低温环境里工作。如果将每个 chiplet 分别放置在独立的稀释制冷机中，那么为了实现 chiplet 之间的互联，就需要将信号线从一个制冷机的低温环境引出到室温，再进入另一台制冷机的低温环境。

这种“低温 ↔ 室温 ↔ 低温”的信号传输路径会引入较大的热负载和噪声，从而破坏量子比特的状态。如果所有 chiplet 都放在同一台稀释制冷机里，那我们就需要一台功率极其庞大的稀释制冷机来容纳数千个 chiplet，而制造这样的大规模稀释制冷机本身就是全新的挑战。

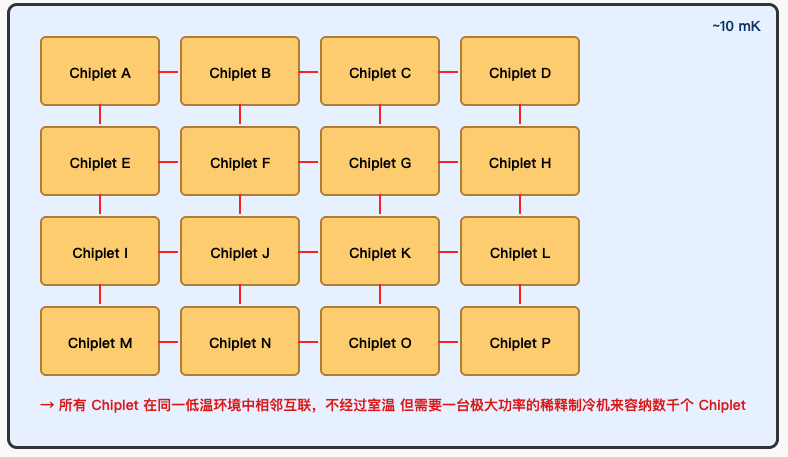
图：Chiplet跨稀释制冷机互联会引入额外热噪声，需要注意的是，实际的互联拓扑并不一定是相邻 Chiplet 两两直接连接。图中所示的相邻互联方式仅用于演示。

图: 多个Chiplet 被放置在同一稀释制冷机内，并在低温环境下直接互联。这种集中式方案意味着需要一台超大功率的稀释制冷机来容纳并维持大量 Chiplet 的工作温度。需要注意的是，实际的互联拓扑并不一定是相邻 Chiplet 两两直接连接，图中所示的相邻互联方式仅用于演示。

因此，未来要么找到新的办法来抑制跨稀释制冷机互联的噪声，要么就得在稀释制冷机的规模化上突破。就目前的科学和工程现状来看，后者，即研发更大功率、更大空间的低温稀释制冷机，似乎是更可行的方向。

总结

如果采用 chiplet 设计 + 片间互联的方案，那么在量子芯片层面上需要跨越的技术鸿沟，就是如何把单片量子比特从数百扩展到数千。

好消息是，半导体已经是一棵“点亮的科技树”，相关工艺还在持续进步。比如，可以借鉴先进封装中的 3D 堆叠工艺来制造量子芯片，从而提高布线密度和互联能力。同时，超导材料工艺的优化、多路复用设计、芯片架构设计的改进（如更高效的耦合器、更合理的频率规划）也都会帮助我们突破这一关口。

所以，单个小芯片从数百到数千个物理量子比特这一阶段，难度虽然不小，但这一步主要还是工程瓶颈，整体上看起来还是比较乐观的。目前，IBM已造出了单片拥有1000个物理量子比特的芯片，不过由于芯片面积很大，将不可避免的面临量产时良品率以及芯片内量子比特可靠性的挑战。

制冷系统

由于超导量子比特的能级差非常微小，量子态极易受到外界环境的扰动而退相干。目前已知的主要干扰因素包括：

被动热源：量子比特虽然在接近绝对零度的环境里，但它必须通过导线和室温的电子设备相连。导线就像一根“热桥”，会把高温环境的热量带到低温区。
主动热源：操控量子比特需要发射微波脉冲，脉冲会沿着导线传输。在传输和衰减的过程中，总会有能量转化为热量，积累起来就会加热环境。
热辐射：即使导线和材料都隔离处理过，量子芯片和外界之间仍然存在电磁辐射耦合，高温的环境会向低温的芯片“辐射热量”。

图：量子比特的三大热干扰源

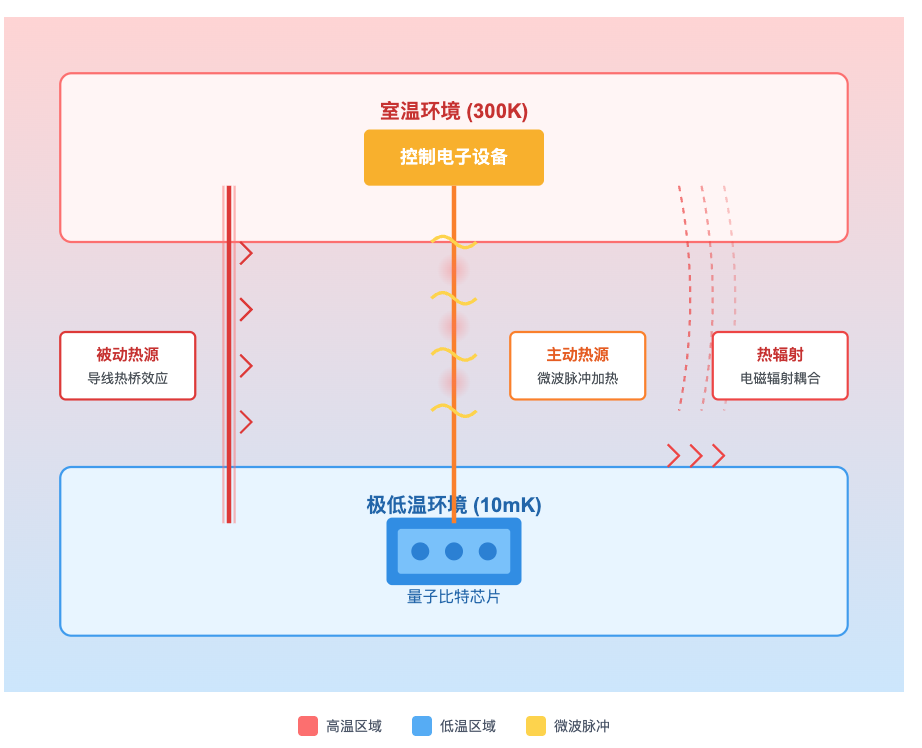
为了尽量隔绝这些影响，现行做法是：

选用热导率、电导率合适的材料制作导线；
在信号路径中加入滤波器和衰减器，削弱非必要频段以及控制信号传输所逸散的能量；
使用稀释制冷机进行分级降温（不是直接从室温降到 10 mK，而是依次经过室温→50 K→4 K→1 K→100 mK→10 mK），逐步屏蔽热源。

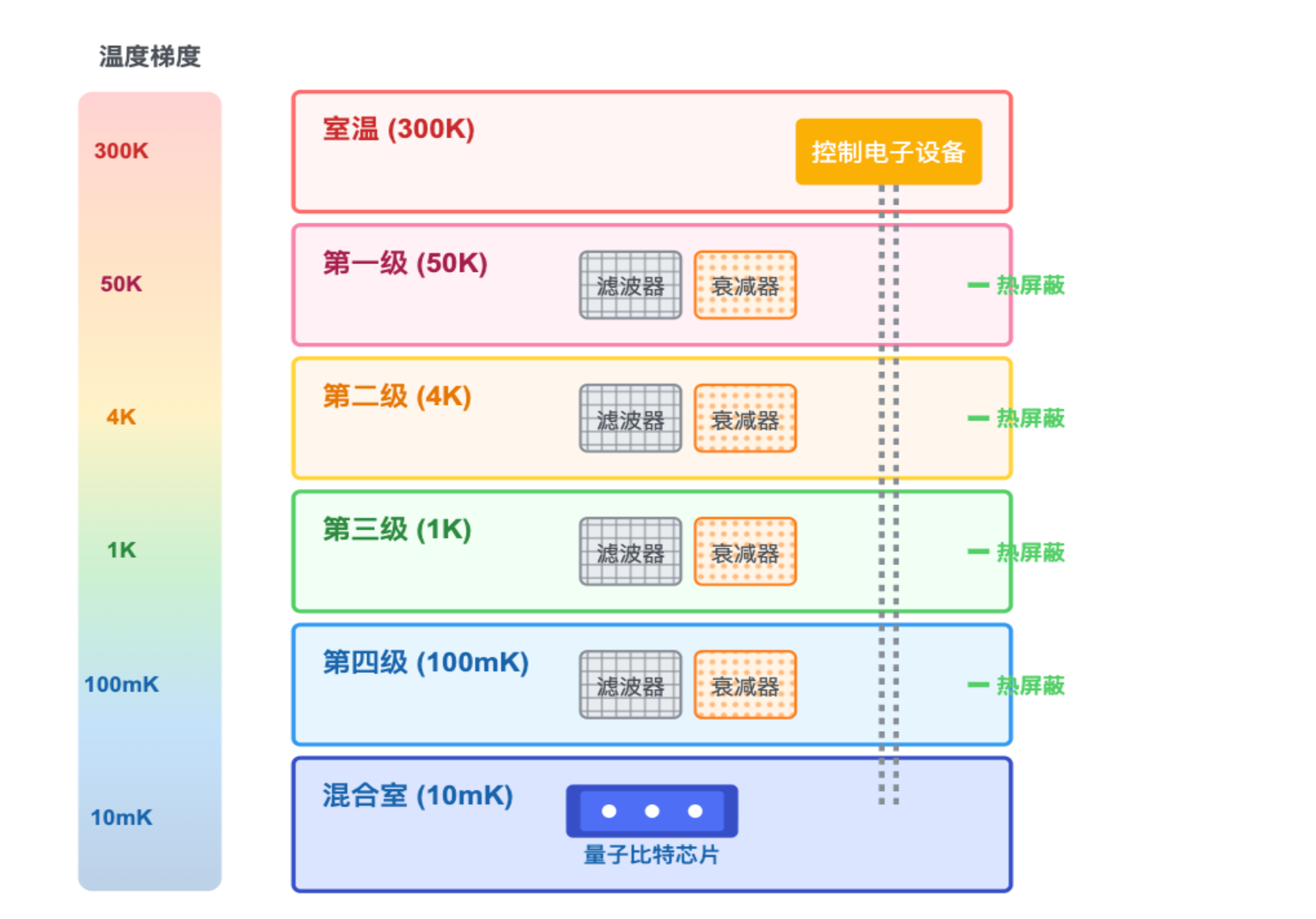
图：稀释制冷机分级降温系统。分级降温的作用有（1）每一级温度平台都起到热缓冲作用，逐步隔离高温环境的热负载；（2）滤波器过滤掉不必要的频率成分，减少噪声干扰；（3）衰减器降低信号强度，同时吸收多余能量，防止加热低温区；（4）热屏蔽层阻挡上级的热辐射，保护下级的低温环境

这种方式目前大致可以支撑数百个物理量子比特。但如果要构建百万级量子比特（比如由数千片、每片数千比特的 chiplet 组成），问题就显现出来了：每个量子比特都需要对应的导线、衰减器、滤波器，数量会随比特数近似线性增加。虽然单根导线的热泄漏量不大，但当导线、滤波器数量扩展到百万量级时，累积的热负载将远远超过制冷机的极限。当然，应对这一挑战，除了需要研发功率更大的稀释制冷机外，也需要探索如何利用多路复用技术、低温 CMOS 电路以及低温超导电子学来降低布线与能耗开销。

总之，现有稀释制冷机的制冷功率和物理空间都严重不足。要支撑百万比特的系统，制冷机的功率至少需要提升百万倍以上。但这种超大功率、超大体积的稀释制冷机目前还不存在。

图：从百比特到百万比特，制冷系统的扩展性挑战

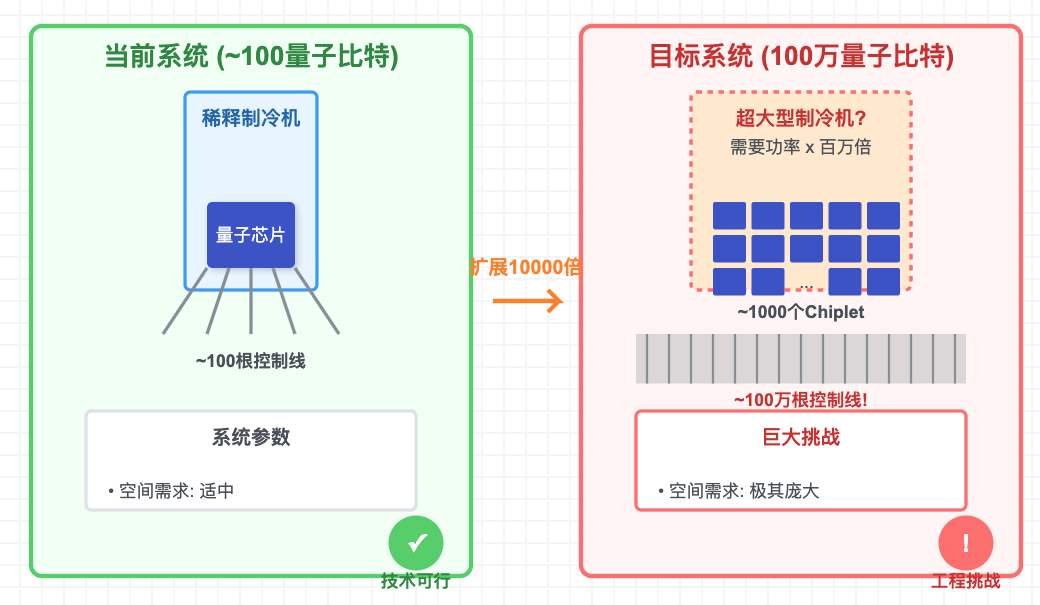
如果采用 “chiplet 设计” + “低温片间互联” 的方案，那么制冷系统就是一道必须跨越的工程大关，所需的研发投入极为庞大（很可能在数十亿美元量级）。

量子比特控制系统

如前文所述，每个超导量子比特都需要用微波信号来进行控制，并且不同的比特必须分配到不同的控制频率。随着量子比特数量从数百扩展到数百万，控制系统会面临几个明显的挑战：

频率拥挤：微波的频谱范围是有限的，比特数增加后，频率间隔被迫减小。相邻频率太接近时，控制信号可能互相干扰，造成串扰问题。

图：相邻频率太接近时，控制信号可能互相干扰，造成串扰问题。

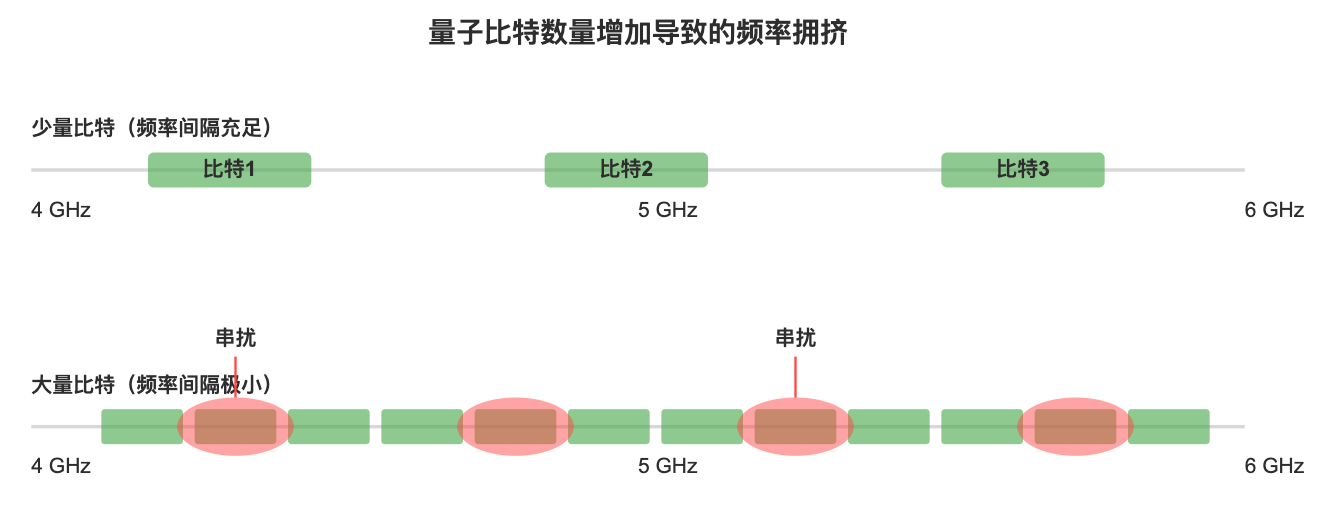
精度要求提高：频带变窄意味着控制信号必须更加稳定，否则会“溢出”到相邻比特。对频率稳定度和相位噪声的要求变得更严格。

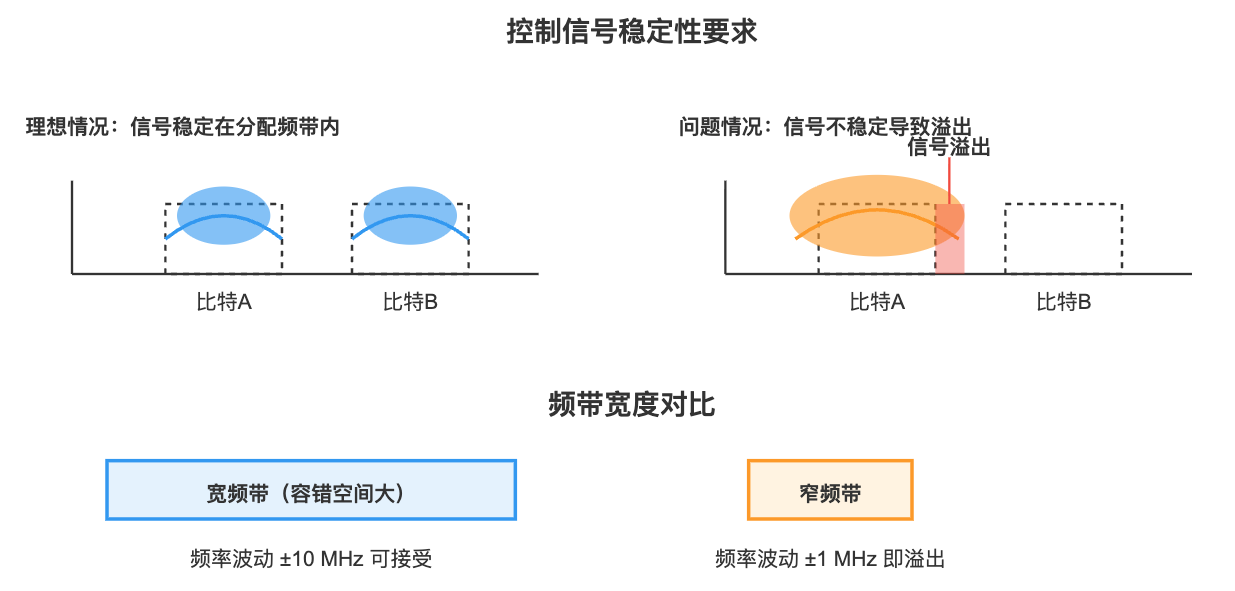
图：频带变窄后，对控制信号的频率稳定度和相位噪声要求大幅提高微小的频率漂移都可能造成信号溢出到相邻量子比特

控制复杂度飙升：每个量子比特都需要独立的脉冲控制（幅度、相位、时序）。如果有百万个量子比特，就意味着要有百万个独立控制通道。目前一个通道的硬件成本大约在 10 万元/个，长远目标是降到 1000 元/个，否则成本无法承受。

图：如果有百万个量子比特，就意味着要有百万个独立控制通道

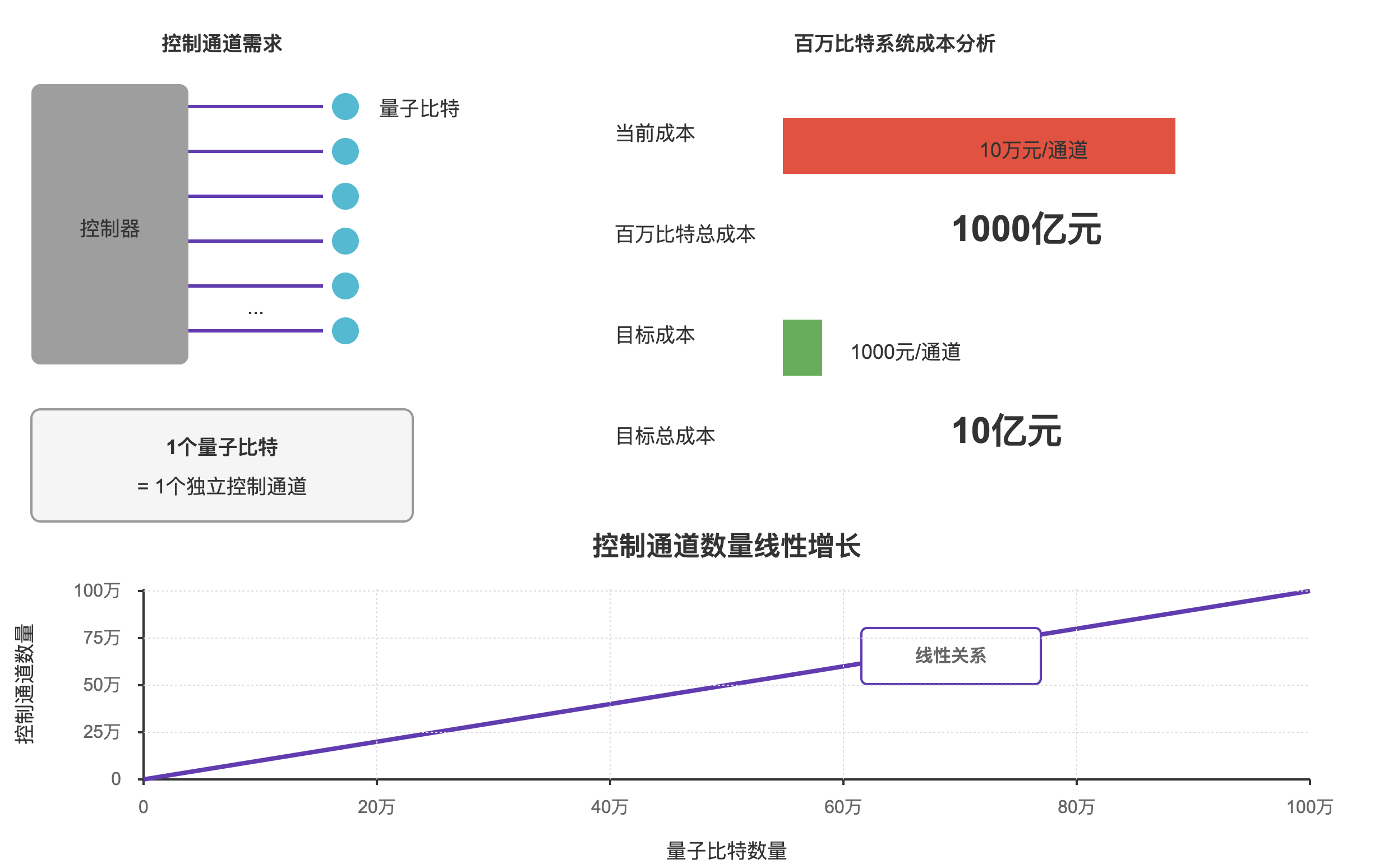
这些问题本质上都是工程瓶颈。在小规模系统里已经显现，规模扩大后复杂度呈现线性增长。

不过，这一方向的挑战相比其他问题而言，业界普遍认为相对乐观，原因主要有：

频率拥挤的规律：实验表明，在几十比特范围内（大约 60 比特以内），频率分配的复杂度增加较快，但随着比特数进一步增加，可以通过巧妙的频率复用和比特布局，使复杂度趋于可控。因此“频率拥挤”并不一定是无法跨越的硬障碍。
门精度要求有限：量子计算并不要求无限精度，只要双比特门的保真度能稳定在 99.99% 左右，就足以支撑量子纠错。虽然对控制系统的噪声要求仍然很高，但这是现有半导技术可以实现的。只是目前能实现这种精度的高速数模转换器（DAC）成本过高，未来是否能够依靠大规模制造降低成本仍待测量。
硬件成本优化的可能性：目前控制使用的是超导同轴线缆、转接头、衰减器和滤波器，这些器件成本高、体积大。一个潜在方向是借鉴半导体产业的柔性基板工艺，直接在低成本材料上批量制造集成化的低温布线，从而显著降低成本和体积。

小结一下，控制系统是另一道必须跨越的工程瓶颈：百万量级量子比特需要百万独立控制通道，频率分配、信号精度和成本压降都是关键难点，虽然相对其他方面的问题更加乐观，但依然需要长期的工程投入与技术迭代。

纠错系统

要让量子比特和门保真度满足完成像分解 RSA 这样的大规模计算的要求，就必须依靠量子纠错：用上千个物理比特来构成 1 个逻辑比特。

量子纠错的理论框架已经成熟，能够显著提升逻辑比特的相干时间和门保真度。例如谷歌在 Willow 项目中，就展示了通过纠错方法获得更稳定的逻辑比特。

在 Willow 处理器中，一个逻辑量子比特并不是由单个物理比特直接表示，而是由一个二维物理比特阵列共同编码。阵列中包含两类比特：

数据比特：用于承载逻辑量子态；
辅助比特：通过周期性操作来检测数据比特之间是否出现了错误。

这些辅助比特的测量结果不会直接揭示逻辑态本身，但能反映出系统中是否发生了位翻转或相位翻转等错误。结合解码算法，系统可以判断错误发生的位置并进行修正。在 Willow 的实验中，研究人员首次在硬件上验证了这样一个关键特性：当物理比特的误差率降低到阈值以下时，只要工程上允许，理论上可以通过持续增加编码规模来持续延长逻辑量子比特的有效相干时间，并持续提高逻辑门的保真度。换句话说，相干时间和门保真度的最终限制主要来源于工程资源，而非基本物理定律。

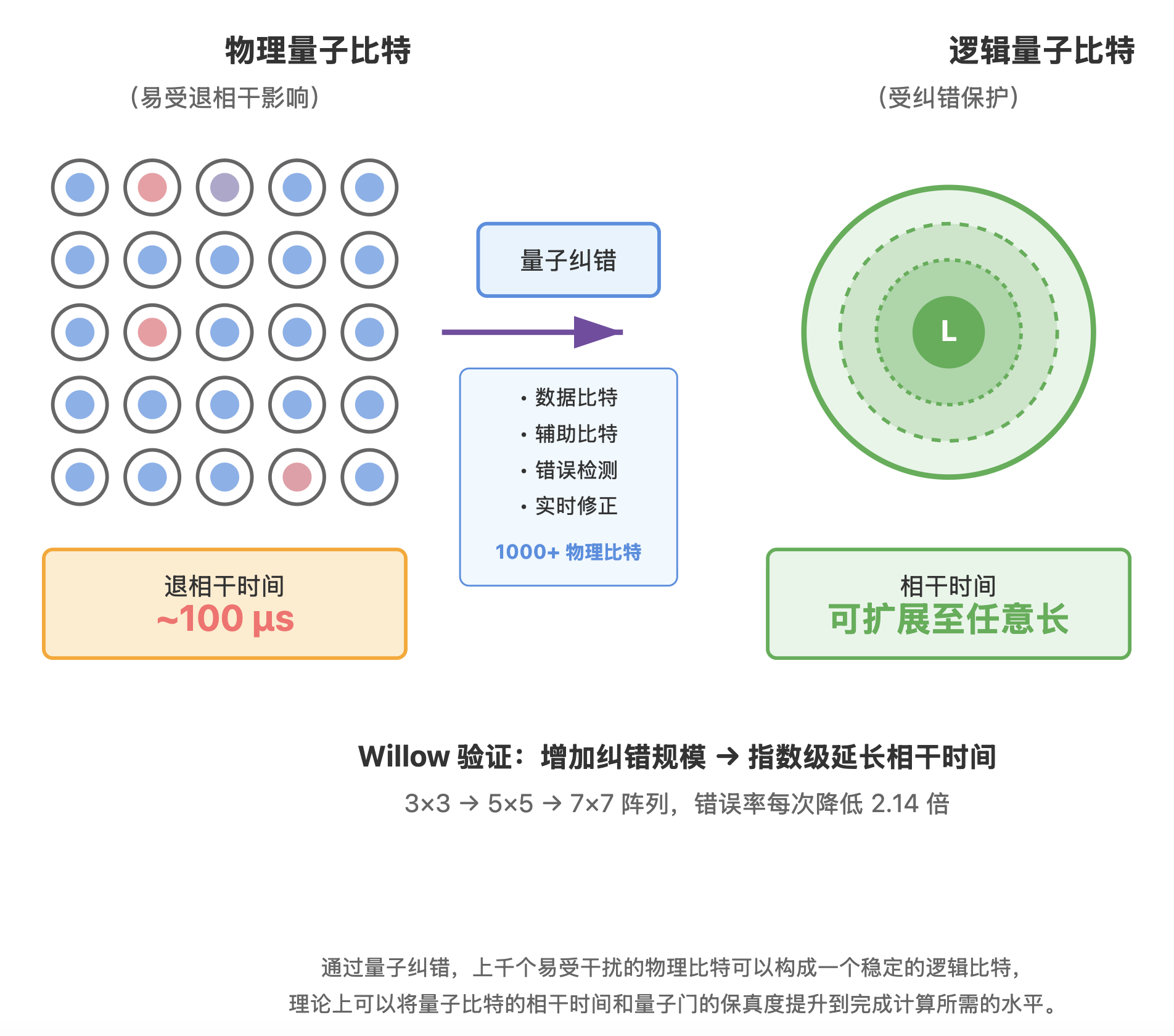
图：多个易受干扰的物理比特可以构成一个稳定的逻辑比特，理论上通过扩大用于纠错的物理量子比特的规模可以将相干时间延长到完成大规模量子计算所需的任意时长。

不过，在工程实现上，解码算法必须是实时的：如果错误累积过快，将超出可恢复范围。随着比特数量增加，纠错开销呈非线性增长，对经典硬件提出极高的算力和延迟要求。好在纠错计算本身可以高度并行，理论上可以通过增加算力（即“堆钱”）来缓解瓶颈。

挑战不仅在物理层面，还在于软硬件一体化工程：由于量子比特持续产生随机错误无法在运行前预知，电路必须根据现场检测到的错误信息动态调整后续操作。同时，纠错系统还要实现逻辑比特的实时调度与校准，并在极低延迟下完成并行解码。这些要求叠加在一起，使得容错量子计算不仅仅是一个硬件难题，还是一个规模极大、复杂度极高的系统工程。

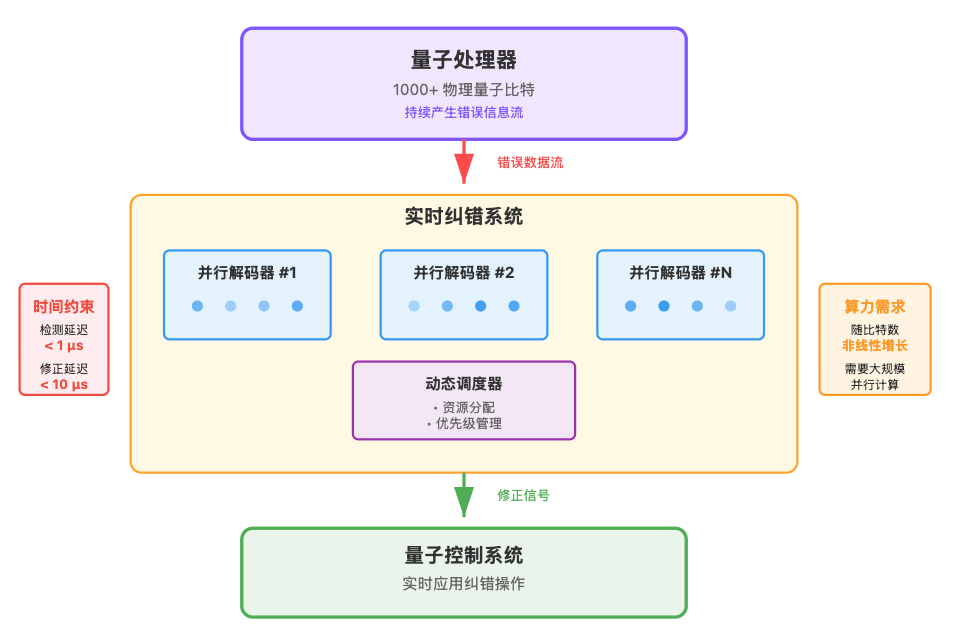
图：量子纠错不仅是物理问题，更是极具挑战的系统工程：需要在微秒级时间内完成错误检测、并行解码和实时修正，算力需求随系统规模非线性增长，但可通过增加硬件资源（"堆钱"）来解决。

总之，量子纠错系统是一个必须跨越的门槛：它要求上千物理比特组成 1 个逻辑比特，并依赖实时、并行的纠错与动态调度，这对软硬件一体化提出极高要求，是极具挑战性的系统工程。但整个过程没有无法解决的科学上的限制，更多是系统工程的挑战。

破解 RSA2048 的量子计算机高概率在 203X 年出现

综上所述，要制造出能够破解 RSA‑2048 的百万量子比特计算机，科学问题在于退相干和门错误不可避免，但量子纠错理论已提供明确的解决路径；真正的难点在工程层面，包括冷却、控制、布线、能耗以及量子纠错的实时实现。随着规模扩展，这些问题会呈现非线性放大，尤其是串扰、纠错开销和能耗，但在一定规模后可通过模块化设计和片间互联让复杂性进入区域线性阶段。总体而言，没有科学上的“死胡同”，但工程挑战极大，需要长期积累和巨额投入。目前行业内普遍预期这样的量子计算机会以很高概率在 203X 年出现，我们是认同这一判断的。

附录1：叠加态和纠缠的数学表述

叠加态和坍缩的向量表达

在量子力学中，对于单个量子态，我们可以以向量的形式

$$ |\psi\rangle = \alpha |S_0\rangle + \beta |S_1\rangle $$

其中：

$|S_0\rangle$ 和 $|S_1\rangle$ 是该量子系统的两个可能状态；
$\alpha$ 和 $\beta$ 称为复数概率振幅，其模平方给出测量时得到对应状态的概率，且满足 $|\alpha|^2+|\beta|^2=1$。

量子计算机选取物理系统中的两个可区分的物理量子态来作为信息载体，分别记作 $|0\rangle$ 和 $|1\rangle$。因此，一个量子比特（qubit）的状态可写为：

$$ |\psi\rangle = \alpha |0\rangle + \beta |1\rangle $$

量子纠缠的向量表达

如果两个比特发生了 “互补取值纠缠”，也就是我们前面举过的“两个比特的值必须不同”的情况，那么系统的状态就是

$$ |\psi\rangle = \alpha |01\rangle + \beta |10\rangle $$

其中 $\alpha$ 和 $\beta$ 是复数概率幅，满足归一化条件 $|\alpha|^2+|\beta|^2=1$。

这意味着：测量结果为“01”的概率是 $|\alpha|^2$，测量结果为“10”的概率是 $|\beta|^2$，而“00”与“11”的概率严格为 0。可以看出，量子纠缠其实是叠加态在多维基底的扩展。

量子态的波函数表达

量子态也可以用波的形式进行描述，波函数的模方给出了坍缩到某个具体状态的概率。我们以被关在一维盒子里的粒子（两端是不可逾越的墙壁）为例，粒子的波在两端反射并相互叠加（类似于声音在两个墙壁之间回荡），波函数表现为驻波。

$$ \psi_n(x,t) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right) e^{-i\omega_n t} $$

其中 $t$ 是时间，$x$ 是粒子的位置，$L$ 是盒子的长度（粒子运动的范围），$n$ 是量子数（1,2,3…，决定波函数有几个波峰波谷），$k = \frac{n\pi}{L}$ 是波数（即空间频率），$\lambda = \frac{2\pi}{k} = \frac{2L}{n}$ 是波长（即空间周期），$\omega$ 是角频率，波的时间频率 $f = \frac{\omega}{2\pi}$ 。粒子在 $t$ 时刻出现在位置 $x$ 的概率为 $|\psi(x,t)|^2$。时间推移只为整个波函数添上一串旋转的相位因子，不影响概率分布。

图：t=0 时波函数的实部，展示波函数随位置的空间分布。

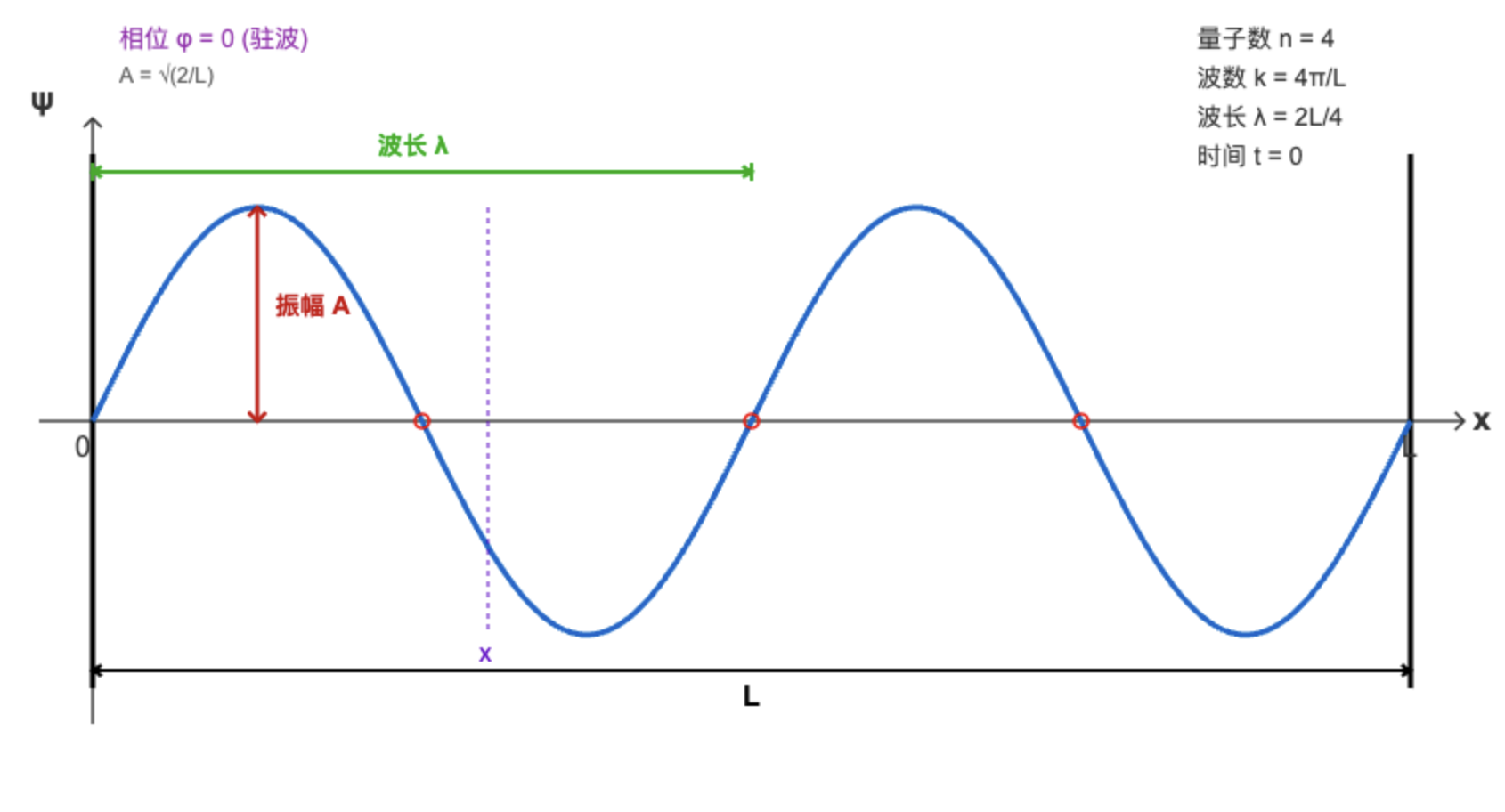
量子态的波函数表达与向量表达的关系

有些读者可能会疑惑：态矢量的形式 $|\psi\rangle = \alpha |S_0\rangle + \beta |S_1\rangle$ 与波函数形式 $\psi_n(x,t)$ 看起来好像没有直接联系。其实它们是同一个量子态在不同“坐标系”下的两种表现方式。

要描述某个时刻（假设 $t=0$）的量子态 $|\psi\rangle$，必须先选一组基底。

第一种方式，使用连续的位置基 ${|x\rangle}_{0<x<L}$，这时抽象的量子态可被描述为 $\psi(x)=\langle x | \psi \rangle$，称为波函数，它对每一点 $x$ 分配一个复数振幅。
第二种方式，使用离散的能量基 ${|n\rangle}$，这时抽象的量子态可被描述为 $|\psi\rangle = \sum_n c_n|n\rangle$，其中 $c_n=\langle n|\psi\rangle$，它为每个能量本征态分配一个复数振幅。

两种坐标可以互相转化：

$$ \psi(x)=\sum_n c_n\sqrt{\frac{2}{L}}\sin(\frac{n\pi x}{L}) $$

这两种写法只是视角不同，本质上描述的是同一个物理量。

附录2：量子算法如何威胁经典密码

为了让不熟悉数学或物理的读者也能理解，本部分会尽量减少使用复杂的数学公式。这样做可能会带来一些细节上的不精确，但不会影响整体理解。

Grover算法：加速搜索问题

经典搜索的瓶颈

假设你有一个黑盒函数 $f(x)$，它能判断某个输入 $x$ 是否是正确答案：

$f(x) = 1$：表示 $x$ 是目标
$f(x) = 0$：表示 $x$ 不是目标

如果 $x$ 是一个 32 位整数，可能的取值有 $2^{32}$ 种。在经典计算机中，只能一个一个尝试 $f(x)$，最坏情况下需要 $2^{32}$ 次。

量子计算如何加速搜索？

量子计算机通过叠加态和干涉，把搜索复杂度从 $O(N)$ 降低到 $O(\sqrt{N})$。Grover算法的核心逻辑如下：

构造叠加态。量子计算机可以让变量 x同时表示所有可能值的叠加态，也就是 ($x = 0, 1, 2, \cdots, 2^{32} - 1$)。如果把这些值代入 $f(x)$，那么 $f(x)$ 的结果也会是所有可能输出的叠加态。对于某些 $x$，$f(x)$ 的值是 0；对于另一些 $x$，$f(x)$ 的值是 1。
标记正确答案（Oracle 操作）。Grover算法的关键是“标记正确答案”。在量子计算中，这个标记并不是直接告诉你答案，而是通过操作让正确答案在量子力学层面变得特殊。比如，我们对 $f(x) = 1$ 的那些 $x$（即正确答案）做一个特殊处理：改变它的“相位”。相位是量子态的一个属性，虽然它本身不可见，但可以通过后续操作影响量子态坍缩时的概率分布。这一步相当于给正确答案做了一个“隐形标记”。干涉放大正确答案的概率。
通过干涉放大正确答案的概率。接下来，通过相长干涉，让正确答案的振幅逐步放大，通过相消干涉，让错误答案的振幅逐步减小。可以把它想象成一个“放大器”，每次操作都让正确答案的存在感变得更强。每次干涉操作都会进一步提高正确答案的概率。经过大约 $\sqrt{N}$ 次 Oracle 操作后，正确答案的概率会接近1。
测量正确答案。最后，通过测量量子态，量子计算机几乎总能返回正确答案。

图：Grover 算法示意图

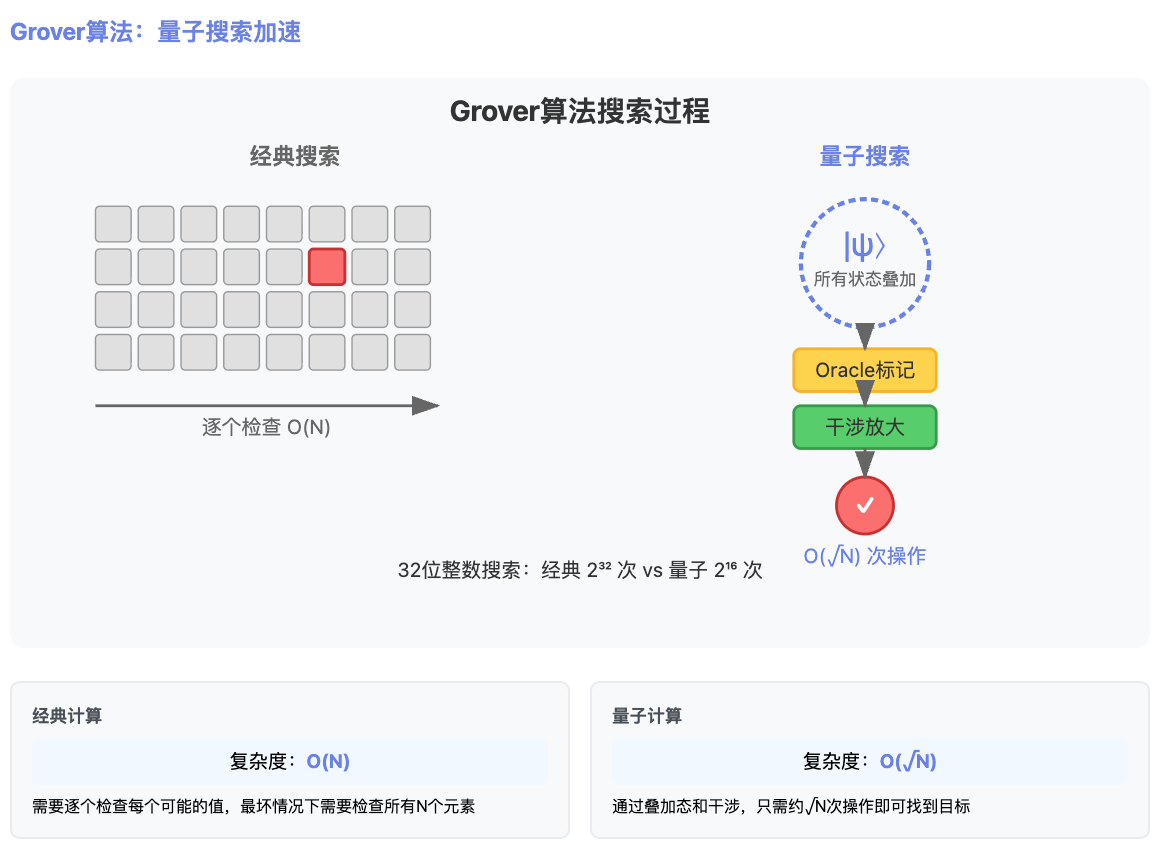
密码学上的应用举例：破解哈希函数

假设你有一个哈希函数 $f(x)$，已知一个哈希值 $H$，想找到某个输入 $x$ 满足 $f(x) = H$。如果 $x$ 是一个 4 字节整数（取值范围为 $2^{32}$），经典计算需要最多尝试 $2^{32}$ 次，而 Grover 算法只需要大约 $2^{16}$ 次。这种加速对密码破解和无序搜索非常有用。

类似地，我们也可以用 Grover 算法加速破解 AES 等对称密码。

Shor算法：加速质因数分解

经典质因数分解的难点

质因数分解是一个经典问题：给定一个大合数 $N$，找到两个整数大于 1 的整数 $p$ 和 $q$，使得 $N = p \times q$。当 $N$ 是两个足够大的质数的乘积时，经典计算机需要尝试大量可能值，时间复杂度呈指数级增长。这就是 RSA 加密的安全基础：分解一个 2048 位的整数几乎是不可能完成的任务。

量子计算如何加速质因数分解？

首先，我们可以通过数论知识将质因数分解问题转化为一个“周期问题”，Shor算法会利用量子傅里叶变换高效提取周期，从而计算出因数。核心逻辑如下：

转化为周期问题

选择一个随机数 $a$，计算 $f(x) \equiv a^x \pmod N$。这个计算会生成一个周期性序列，比如：

$$ f(0) = 1, f(1) = 3, f(2) = 9, f(3) = 27, f(4) = 9, f(5) = 27, \cdots $$
序列每隔一段时间就会重复，这段重复的长度就是周期 $r$。找到这个周期后，就可以快速得到 $N$ 的一个因子，然后再递归拆解 $N$ 的其他因子。

量子傅里叶变换提取周期

在经典计算中找到周期需要一个一个尝试，非常耗时。而量子计算通过叠加态“同时计算”所有可能的 $x$，通过让量子比特在一串受控的模乘运算中积累与周期成比例的相位，并用量子傅里叶变换把这个相位转换成可测量的结果，就能在多项式时间里把函数的周期 $r$ 提取出来。

计算因数

一旦知道了周期 $r$，通过简单的数学公式，就可以快速分解出 $N$ 的因数。具体地，通过计算 $\text{gcd}(a^{r/2}\pm 1, N)$，即可得到 $N$ 的因子。

图：Shor 算法破解 RSA 的示意图

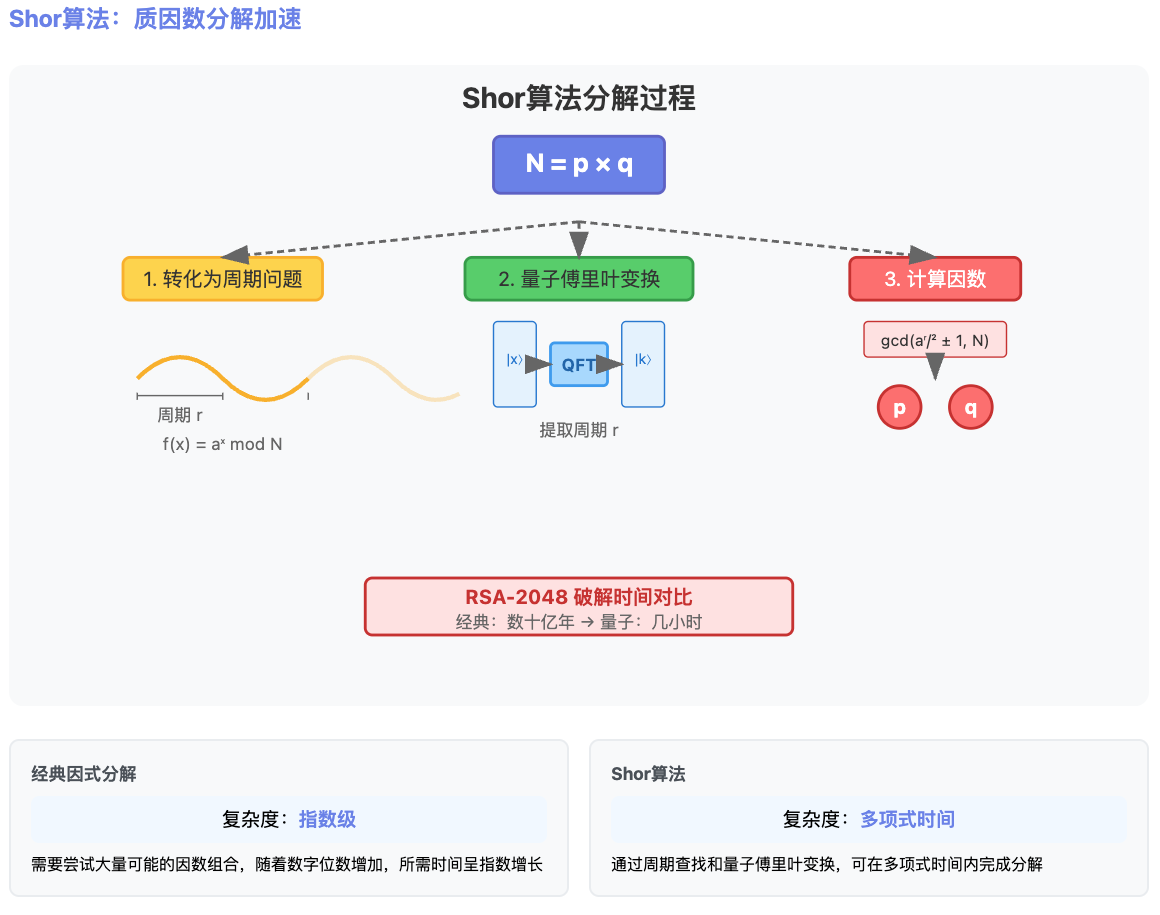
密码学上的应用：RSA 破解

RSA 加密的安全性依赖于大整数质因数分解的困难性。如果用经典计算机分解一个 2048 位的整数，可能需要数十亿年。而 Shor 算法可以在几小时内完成分解，对现代加密体系构成了直接威胁。

导航

Part 1: 量子计算机为什么能加速计算？

叠加态与坍缩

量子纠缠

利用叠加性和纠缠性加速计算

量子计算对不同问题的加速效果

Part 2: 量子计算机是怎样构建出来的？

量子比特在物理上的实现方式

超导量子比特的构建原理

从单比特到超导量子计算的“体系结构”

量子芯片

制冷系统

量子比特控制系统

量子纠错系统

整体架构

构建量子计算机需要科学与工程学结合

Part 3: 构建能破解 RSA 2048 的量子计算机，还有哪些挑战？

量子芯片

布线问题

串扰问题

器件良品率问题

希望的曙光：模块化设计与片间互联

总结

制冷系统

量子比特控制系统

纠错系统

破解 RSA2048 的量子计算机高概率在 203X 年出现

附录1：叠加态和纠缠的数学表述

叠加态和坍缩的向量表达

量子纠缠的向量表达

量子态的波函数表达

量子态的波函数表达与向量表达的关系

附录2：量子算法如何威胁经典密码

Grover算法：加速搜索问题

经典搜索的瓶颈

量子计算如何加速搜索？

密码学上的应用举例：破解哈希函数

Shor算法：加速质因数分解

经典质因数分解的难点

量子计算如何加速质因数分解？

密码学上的应用：RSA 破解

参考文献